A flat (unbanked) curve on a highway has a radius of m. A car rounds the curve at a speed of m/s. What is the minimum coefficient of static friction that will prevent sliding?

In another version of the 'Giant Swing' (see Exercise ), the seat is connected to two cables, one of which is horizontal (Fig. E). The seat swings in a horizontal circle at a rate of rpm (rev/min). If the seat weighs N and an -N person is sitting in it, find the tension in each cable.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Centripetal Force

Tension in Cables

Equilibrium of Forces

A -kg car and a -kg pickup truck approach a curve on a highway that has a radius of m. At what angle should the highway engineer bank this curve so that vehicles traveling at mi/h can safely round it regardless of the condition of their tires? Should the heavy truck go slower than the lighter car?
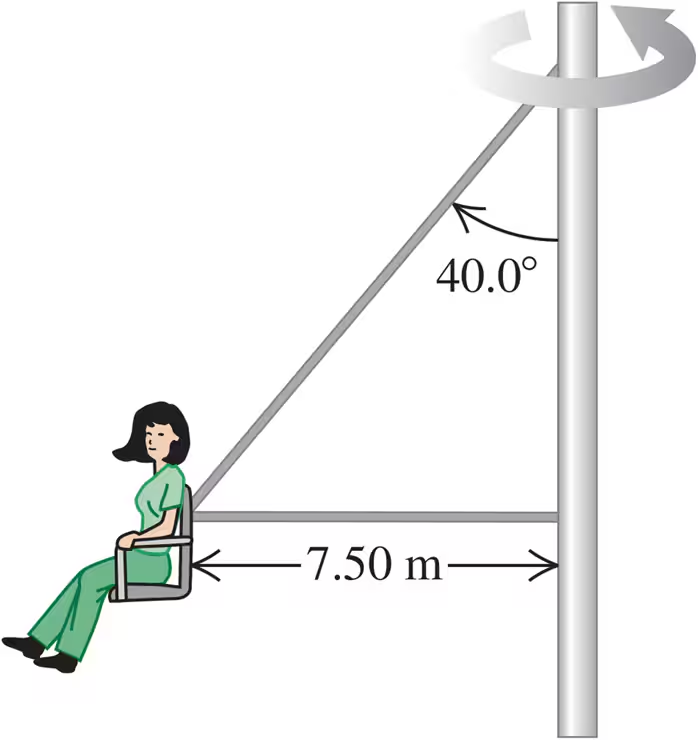
The 'Giant Swing' at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a cable m long, and the upper end of the cable is fastened to the arm at a point m from the central shaft (Fig. E). Find the time of one revolution of the swing if the cable supporting a seat makes an angle of with the vertical.
One problem for humans living in outer space is that they are apparently weightless. One way around this problem is to design a space station that spins about its center at a constant rate. This creates 'artificial gravity' at the outside rim of the station. If the diameter of the space station is m, how many revolutions per minute are needed for the 'artificial gravity' acceleration to be m/s2?
The Cosmo Clock 21 Ferris wheel in Yokohama, Japan, has a diameter of m. Its name comes from its arms, each of which can function as a second hand (so that it makes one revolution every s). Find the speed of the passengers when the Ferris wheel is rotating at this rate.
The Cosmo Clock 21 Ferris wheel in Yokohama, Japan, has a diameter of m. Its name comes from its arms, each of which can function as a second hand (so that it makes one revolution every s). A passenger weighs N at the weight-guessing booth on the ground. What is his apparent weight at the highest and at the lowest point on the Ferris wheel?
