A web page designer creates an animation in which a dot on a computer screen has position r→=[4.0 cm+(2.5 cm/s2)t2]iî+(5.0 cm/s)t jĵ. (a) Find the magnitude and direction of the dot's average velocity between t = 0 and t = 2.0 s.

Verified step by step guidance

1. Identify the position vector r→(t) given in the problem. For this problem, r→(t) = [4.0 cm + (2.5 cm/s^2)t^2]î + (5.0 cm/s)t ĵ.
2. Calculate the position of the dot at t = 0 s using the position vector. Substitute t = 0 into r→(t) to find r→(0).
3. Calculate the position of the dot at t = 2.0 s using the position vector. Substitute t = 2.0 s into r→(t) to find r→(2.0 s).
4. Determine the displacement vector Δr→ by subtracting r→(0) from r→(2.0 s). Δr→ = r→(2.0 s) - r→(0).
5. Calculate the magnitude and direction of the average velocity vector v→_avg by dividing the displacement vector Δr→ by the time interval Δt (which is 2.0 s in this case). v→_avg = Δr→ / Δt. The magnitude is found by calculating the norm of v→_avg, and the direction can be found by calculating the angle of v→_avg with respect to the positive x-axis.

Key Concepts

Position Vector

The position vector, denoted as r→, describes the location of an object in space relative to a reference point. In this case, it is expressed in terms of time, with components in the i and j directions. Understanding the position vector is crucial for determining how the object's location changes over time, which is essential for calculating velocity.

Average Velocity

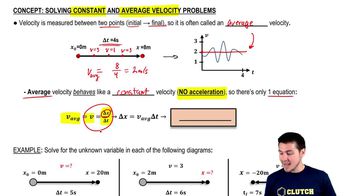
Average velocity is defined as the change in position divided by the time interval over which that change occurs. Mathematically, it is calculated as v_avg = Δr/Δt, where Δr is the difference in position vectors at two time points. This concept is vital for analyzing motion, as it provides insight into the overall speed and direction of an object over a specified time period.

Magnitude and Direction

In physics, the magnitude of a vector represents its size or length, while the direction indicates the orientation of the vector in space. For average velocity, calculating its magnitude involves finding the length of the average velocity vector, and determining its direction requires analyzing the components of the vector. This distinction is important for fully understanding the motion of the dot on the screen.