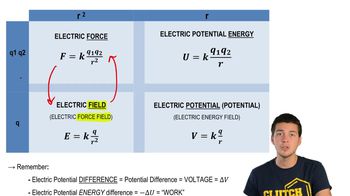
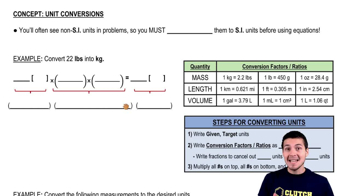
Textbook Question
Why Are We Bombarded by Muons? Muons are unstable subatomic particles that decay to electrons with a mean lifetime of 2.2 ms. They are produced when cosmic rays bombard the upper atmosphere about 10 km above the earth's surface, and they travel very close to the speed of light. The problem we want to address is why we see any of them at the earth's surface. (a) What is the greatest distance a muon could travel during its 2.2@ms lifetime? (b) According to your answer in part (a), it would seem that muons could never make it to the ground. But the 2.2@ms lifetime is measured in the frame of the muon, and muons are moving very fast. At a speed of 0.999c, what is the mean lifetime of a muon as measured by an observer at rest on the earth? How far would the muon travel in this time? Does this result explain why we find muons in cosmic rays? (c) From the point of view of the muon, it still lives for only 2.2 ms, so how does it make it to the ground? What is the thickness of the 10 km of atmosphere through which the muon must travel, as measured by the muon? Is it now clear how the muon is able to reach the ground?
756
views