Here are the essential concepts you must grasp in order to answer the question correctly.
Mean Free Path
The mean free path is the average distance a particle travels between collisions with other particles. In gases, this concept is crucial for understanding how particles interact and move. It depends on factors such as the density of the gas and the size of the particles. At low temperatures, like in liquid helium, the mean free path can be significantly longer due to reduced particle density.
Recommended video:
Root Mean Square (RMS) Speed
The root mean square speed is a measure of the average speed of particles in a gas, calculated from the kinetic theory of gases. It is defined as the square root of the average of the squares of the speeds of all the particles. The RMS speed is directly related to the temperature of the gas, indicating that as temperature increases, the speed of the particles also increases, which is particularly relevant for helium at 4.2 K.
Recommended video:
Root-Mean-Square Speed of Ideal Gases
Average Energy per Atom
The average energy per atom in a gas is derived from the kinetic theory and is proportional to the temperature of the gas. For a monatomic ideal gas, this energy can be calculated using the formula E = (3/2)kT, where k is the Boltzmann constant and T is the temperature in Kelvin. At 4.2 K, this relationship helps determine the energy distribution among helium atoms, which is essential for understanding their behavior in the gas phase.
Recommended video:
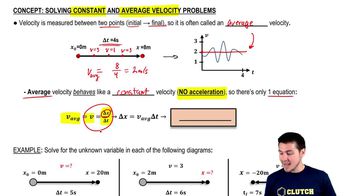
Solving Constant and Average Velocity Problems