Here are the essential concepts you must grasp in order to answer the question correctly.
Isobaric Process
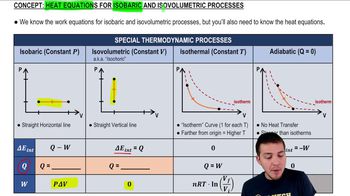
An isobaric process is a thermodynamic process in which the pressure remains constant while the volume and temperature of the gas change. In this scenario, the nitrogen gas expands at a constant pressure of 3.0 atm, which simplifies the calculations for heat transfer, as the work done by the gas can be directly related to the change in volume.
Recommended video:
Heat Equations for Isobaric & Isovolumetric Processes
First Law of Thermodynamics
The First Law of Thermodynamics states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system. In the context of the isobaric expansion, the heat energy transferred to the gas can be calculated by considering both the work done during the expansion and the change in internal energy.
Recommended video:
The First Law of Thermodynamics
Heat Capacity at Constant Pressure (Cp)
Heat capacity at constant pressure (Cp) is the amount of heat required to raise the temperature of a unit mass of a substance by one degree Celsius while maintaining constant pressure. For an ideal gas, this value is crucial for calculating the heat energy transferred during an isobaric process, as it relates the temperature change to the heat added to the system.
Recommended video:
Phase Constant of a Wave Function
 Knight Calc 5th Edition
Knight Calc 5th Edition Ch 19: Work, Heat, and the First Law of Thermodynamics
Ch 19: Work, Heat, and the First Law of Thermodynamics Problem 19
Problem 19 Verified step by step guidance
Verified step by step guidance