Here are the essential concepts you must grasp in order to answer the question correctly.
Speed of Sound
The speed of sound is the rate at which sound waves propagate through a medium, such as air. It varies with temperature; as the temperature increases, the speed of sound also increases. In this scenario, the speed of sound changes from 342 m/s to 346 m/s due to the warming of the air inside the flute, affecting the pitch of the notes produced.
Recommended video:
Frequency and Wavelength
Frequency is the number of oscillations or cycles of a wave that occur in a unit of time, measured in Hertz (Hz). The wavelength is the distance between successive crests of a wave. For a given speed of sound, the relationship between speed (v), frequency (f), and wavelength (λ) is given by the equation v = f * λ. Changes in the speed of sound will affect the wavelength of the notes played.
Recommended video:
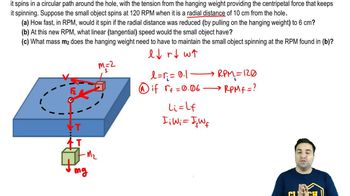
Circumference, Period, and Frequency in UCM
Tuning and Length Adjustment
In musical instruments like flutes, tuning involves adjusting the length of the instrument to match a desired frequency. The pitch of the note produced is inversely related to the length of the air column; a longer column produces a lower pitch. To maintain perfect tuning with the 440 Hz fork after the speed of sound changes, the flutist must extend the tuning joint to adjust the effective length of the flute.
Recommended video:
Spinning on a string of variable length