Here are the essential concepts you must grasp in order to answer the question correctly.
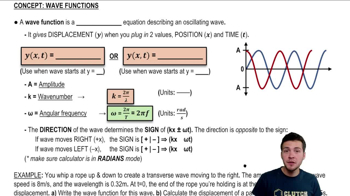
Wave Equation
The wave equation is a second-order partial differential equation that describes the propagation of waves, such as sound or light, through a medium. It is typically expressed as ∂²D/∂t² = v²∂²D/∂x², where D is the displacement, t is time, x is position, and v is the wave speed. Understanding this equation is crucial for analyzing wave behavior and verifying if a given function satisfies the equation.
Recommended video:
Equations for Transverse Standing Waves
Displacement Function
In the context of wave motion, the displacement function D(x,t) represents the position of points in the medium as a function of both space (x) and time (t). The specific form D(x,t) = cx² + dt² indicates a quadratic relationship in space and time, which is essential for determining how the wave propagates. Analyzing this function helps in checking its compliance with the wave equation.
Recommended video:
Wave Speed
Wave speed is the rate at which a wave propagates through a medium and is denoted by v in the wave equation. It can be derived from the wave equation by relating the coefficients of the displacement function to the speed of the wave. In this case, finding the wave speed involves identifying the relationship between the constants c and d in the displacement function, which ultimately determines how fast the wave travels.
Recommended video:
Intro to Waves and Wave Speed