A sound wave is described by D (y,t) = (0.0200 mm) ✕ sin [(8.96 rad/m)y + (3140 rad/s)t + π/4 rad], where y is in m and t is in s. b. Along which axis is the air oscillating?

Key Concepts

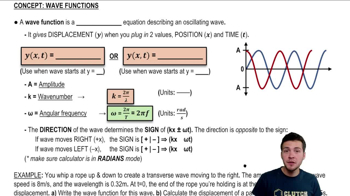
Wave Function

The wave function describes the displacement of a wave at any point in space and time. In this case, D(y,t) represents the displacement of the air particles in the sound wave, which is a sinusoidal function indicating periodic oscillation. The parameters within the sine function, such as wave number and angular frequency, determine the wave's characteristics.

Transverse vs. Longitudinal Waves

Waves can be classified as transverse or longitudinal based on the direction of particle oscillation relative to wave propagation. In longitudinal waves, like sound waves, the oscillation of particles occurs parallel to the direction of wave travel, resulting in compressions and rarefactions. Understanding this distinction is crucial for identifying the oscillation direction in sound waves.

Phase Constant

The phase constant in a wave equation, such as π/4 rad in this case, indicates the initial angle of the wave at time t=0 and position y=0. It affects the starting point of the wave's oscillation but does not change the fundamental nature of the wave. Recognizing the phase constant helps in understanding the wave's behavior at specific points in time and space.