Radioactive Half-Life - Online Tutor, Practice Problems & Exam Prep

Half-life, denoted as t_1/2, is the time required for half of a radioisotope to decay, crucial for understanding radioactive decay. For example, an isotope with a half-life of one day will reduce from 10 grams to 5 grams after one day, then to 2.5 grams after two days, and so on. The fraction remaining can be calculated using the formula ${0.5}^n$, where n is the number of half-lives. This allows for determining both the fraction and the actual amount of the substance remaining.

Radioactive Half-Life Concept 1

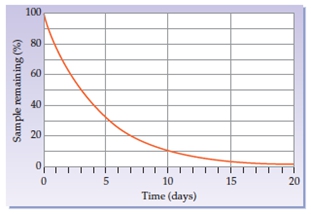
Here we're going to say that half-life, which uses the variable t half, is the amount of time required for half or 50% of a radioisotope to decay. A radioisotope is just the isotopic version of an element that has an unstable nucleus and emits radiation as it decays. Here we're going to say that the radioactive decay of an unknown radioisotope with a half-life of one day is displayed as follows: a half-life is one day, which means that after one day, half of my substance will be gone.

Let's say that we're starting out with some unknown isotope. Remember, our isotope here has x as the symbol, a as the mass number, and z as the atomic number. Let's say that we're starting out with 10 grams of it. Nothing has happened yet, so 0 half-lives have occurred. Initially, I'm starting out with 100% of my substance. Now one day is allowed to pass, and remember, here, a half-life is equal to a day. Now half-lives are not always one day; they vary based on the element. So after one day, I've lost half of my substance, so now I only have 5 grams left. One half-life has passed and all I have left is 50%. I've lost half of what I had.

Another day passes, so I've lost another half. So, starting with 5 grams, another day passes, so now I have only half of that left, which is 2.5 grams. That means 2 half-lives have passed so far, and I only have 25% remaining. Remember, 100% was 10 grams and I only have 2.5 grams. Then another half-life passes, so now I'm losing another half of this 2.5, leaving me with 1.25 grams. So, 3 half-lives have passed, and now I only have 12.5% remaining of the original amount I started with. This is how half-life works, and it keeps going and going and going. I could go to a 4th half-life where I would lose another half of this.

That's the way you have to understand half-life: it's the amount of time it takes to lose half or 50% of my starting material.

Radioactive Half-Life Concept 2

With half-life, we can also determine the amount of radioisotope remaining. Here we're going to say the fractional percentage and final amount of radioisotope after each half-life can be calculated by different means. Alright. So, first we have our fraction formula. This just tells us the fraction remaining of my initial amount. Here, that would just be 0.5n. The 0.5 comes from the fact that a half-life is a half. And when you punch a half into your calculator, it gives you back 0.5. n is just the number of half-lives. One important thing to remember about this is if you also multiply the fraction remaining value by 100%, that will give you the percentage remaining of the radioisotope. So keep that in mind. You can calculate either the fraction remaining or the percentage remaining. Now, we also have our final amount formula. This tells me how much of my final amount is actually remaining. Not a fraction, not a percent, but an actual amount. Let's say you started out with 100 grams of a substance. You could use this formula to tell you how much of that 100 grams is remaining. So here, this would just be brackets with I, this would be your initial amount, times what we just saw our fraction remaining, which is 0.5n. So you can use either formula if you're trying to find either the fraction, percentage, or final amount remaining for a radioisotope.

Radioactive Half-Life Example 1

Here I told that sodium-24, a radioisotope used in examining human circulation, has a half-life of about 15 days. Approximately, what percentage of a sample will remain after 3 months if a month is considered 30 days? Alright. So, they're asking for the percentage remaining. Remember, the percentage remaining is just your fraction remaining, so \( 0.5^n \times 100\% \). Here we have to figure out how many half-lives have occurred. So here we're going to say 3 months have passed and each month is 30 days. That's a total of 90 days. Each half-life is 15 days. So if I do \( \frac{90}{15} \), it gives me back 6. That is the number of half-lives that have occurred. So then all we do here is we're going to say \( 0.5^6 \times 100\% = 1.5625\% \). This is the percentage remaining of my radioisotope.

The half-life of arsenic-74 is about 18 days. If a sample initially contains 100.00 mg arsenic-74, what mass (in mg) would be left after 72 days?

• A. 0.0625 mg
• B. 6.25 mg
• C. 25 mg
• D. 12.5 mg
• E. 50 mg

The half-life of iodine-131, an isotope used in thyroid therapy, is 8.021 days. What percentage of iodine-131 remains in a sample that is estimated to be 40.11 days old?

• A. 3.125%
• B. 0.03125%
• C. 96.87%
• D. 87.06%
• E. 2.236%

What is the concentration of a CO₂ in a container after 4 half-lives if 0.325 mol of CO2 is initially placed into a 5.0 L reaction vessel?

• A. 0.020 M
• B. 4.06×10^–3 M
• C. 8.1×10^–3 M
• D. 0.325 M

What is the half-life of the radioisotope that shows the following plot of remaining percentage vs. time?

• A. 3 days
• B. 5 days
• C. 4 days
• D. 10 days

Here’s what students ask on this topic:

What is the definition of radioactive half-life?

Radioactive half-life, denoted as t_1/2, is the amount of time required for half of a radioisotope to decay. This means that after one half-life, 50% of the original radioactive substance will have transformed into another element or isotope. The concept is crucial for understanding the rate at which radioactive materials decay and is used in various fields such as nuclear medicine, radiometric dating, and nuclear power.

How do you calculate the remaining amount of a radioisotope after a certain number of half-lives?

The remaining amount of a radioisotope after a certain number of half-lives can be calculated using the formula:

$A_f=A_i*\; (0.5)n$

where $A_f$ is the final amount, $A_i$ is the initial amount, and $n$ is the number of half-lives. For example, if you start with 100 grams of a substance and 3 half-lives have passed, the remaining amount would be:

$100\; *\; (0.5)3=\; 12.5$ grams.

What is the formula to calculate the fraction of a radioisotope remaining after n half-lives?

The fraction of a radioisotope remaining after $n$ half-lives can be calculated using the formula:

$(0.5)n$

Here, $n$ represents the number of half-lives. For example, if 4 half-lives have passed, the fraction remaining would be:

$(0.5)4=\; 0.0625$

This means 6.25% of the original amount remains.

How does the half-life of a radioisotope affect its decay rate?

The half-life of a radioisotope directly affects its decay rate. A shorter half-life means the substance decays more quickly, while a longer half-life indicates a slower decay rate. For example, a radioisotope with a half-life of one day will lose half of its mass every day, whereas one with a half-life of a year will take much longer to decay. Understanding the half-life helps in predicting how long a radioactive substance will remain active and is crucial for applications in medicine, archaeology, and nuclear energy.

Can the half-life of a radioisotope change over time?

No, the half-life of a radioisotope is a constant property and does not change over time. It is determined by the nature of the radioactive decay process and the specific isotope. External factors such as temperature, pressure, or chemical state do not affect the half-life. This constancy allows scientists to use half-life as a reliable measure for dating materials and understanding the behavior of radioactive substances.