If 4 percent of a population in equilibrium expresses a recessive trait, what is the probability that the offspring of two individuals who do not express the trait will express it?

Consider a population in which the frequency of allele A is p = 0.7 and the frequency of allele a is q = 0.3 and where the alleles are codominant. What will be the allele frequencies after one generation if the following occurs?
wAA = 1, wAa = 0.99, waa = 0.98
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
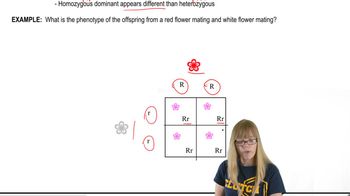
Allele Frequency

Codominance
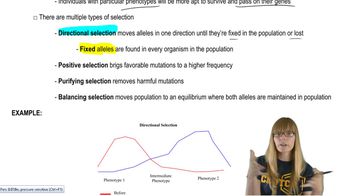
Fitness and Selection Coefficients
Consider a population in which the frequency of allele A is p=0.7 and the frequency of allele a is q=0.3 and where the alleles are codominant. What will be the allele frequencies after one generation if the following occurs?
wAA=1, wAa=0.9, waa=0.8
Consider a population in which the frequency of allele A is p = 0.7 and the frequency of allele a is q = 0.3 and where the alleles are codominant. What will be the allele frequencies after one generation if the following occurs?
wAA = 1, wAa = 0.95, waa = 0.9
Consider a population in which the frequency of allele A is p = 0.7 and the frequency of allele a is q = 0.3 and where the alleles are codominant. What will be the allele frequencies after one generation if the following occurs?
wAA = 0.8, wAa = 1, waa = 0.8
If the initial allele frequencies are p = 0.5 and q = 0.5 and allele a is a lethal recessive, what will be the frequencies after 1, 5, 10, 25, 100, and 1000 generations?
Under what circumstances might a lethal dominant allele persist in a population?
