Carbon disulfide has a vapor pressure of 363 torr at 25 °C and a normal boiling point of 46.3 °C. Find ΔH_vap for carbon disulfide.

Verified step by step guidance

1. Identify the Clausius-Clapeyron equation: \( \ln \left( \frac{P_2}{P_1} \right) = -\frac{\Delta H_{\text{vap}}}{R} \left( \frac{1}{T_2} - \frac{1}{T_1} \right) \), where \( P_1 \) and \( P_2 \) are the vapor pressures at temperatures \( T_1 \) and \( T_2 \), respectively, and \( R \) is the ideal gas constant.
2. Recognize that the normal boiling point is the temperature at which the vapor pressure equals 1 atm (760 torr). Thus, \( P_2 = 760 \text{ torr} \) and \( T_2 = 46.3 \degree C \) (convert to Kelvin by adding 273.15).
3. Use the given vapor pressure at 25 °C: \( P_1 = 363 \text{ torr} \) and \( T_1 = 25 \degree C \) (convert to Kelvin by adding 273.15).
4. Substitute the known values into the Clausius-Clapeyron equation to solve for \( \Delta H_{\text{vap}} \).
5. Rearrange the equation to isolate \( \Delta H_{\text{vap}} \): \( \Delta H_{\text{vap}} = -R \cdot \frac{\ln \left( \frac{P_2}{P_1} \right)}{\left( \frac{1}{T_2} - \frac{1}{T_1} \right)} \).

Key Concepts

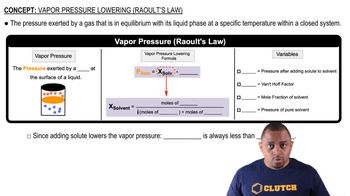
Vapor Pressure

Vapor pressure is the pressure exerted by a vapor in equilibrium with its liquid or solid phase at a given temperature. It reflects the tendency of particles to escape from the liquid phase into the vapor phase. A higher vapor pressure indicates a greater volatility of the substance, which is crucial for understanding phase changes and calculating thermodynamic properties like enthalpy of vaporization.

Enthalpy of Vaporization (ΔH_vap)

The enthalpy of vaporization (ΔH_vap) is the amount of energy required to convert a unit quantity of a liquid into vapor at constant temperature and pressure. It is a critical parameter in thermodynamics that helps quantify the energy changes associated with phase transitions. This value can be determined using the Clausius-Clapeyron equation, which relates vapor pressure and temperature to ΔH_vap.

Clausius-Clapeyron Equation

The Clausius-Clapeyron equation describes the relationship between the vapor pressure of a substance and its temperature, allowing for the calculation of the enthalpy of vaporization. It is expressed as d(ln P)/dT = ΔH_vap/(RT²), where P is the vapor pressure, T is the temperature, R is the ideal gas constant, and ΔH_vap is the enthalpy of vaporization. This equation is essential for solving problems involving phase changes and thermodynamic properties.