Which evaporates more quickly: 55 mL of water (H2O) in a beaker or 100 mL of acetone [(CH3)2CO] in an identical beaker under identical conditions? Is the vapor pressure of the two substances different? Explain.
Ethanol has a heat of vaporization of 38.56 kJ/mol and a normal boiling point of 78.4 °C. What is the vapor pressure of ethanol at 15 °C?
 Verified step by step guidance
Verified step by step guidance
Verified Solution
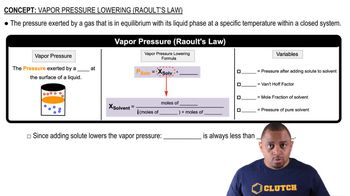
Key Concepts
Heat of Vaporization

Boiling Point

Vapor Pressure
Suppose that 0.95 g of water condenses on a 75.0-g block of iron that is initially at 22 °C. If the heat released during condensation goes only to warming the iron block, what is the final temperature (in °C) of the iron block? (Assume a constant enthalpy of vaporization for water of 44.0 kJ/mol.)
This table displays the vapor pressure of ammonia at several different temperatures. Use the data to determine the heat of vaporization and normal boiling point of ammonia.
Temperature (K) Pressure (torr)
200 65.3
210 134.3
220 255.7
230 456.0
235 597.0
Benzene has a heat of vaporization of 30.72 kJ/mol and a normal boiling point of 80.1 °C. At what temperature does benzene boil when the external pressure is 445 torr?
Carbon disulfide has a vapor pressure of 363 torr at 25 °C and a normal boiling point of 46.3 °C. Find ΔHvap for carbon disulfide.
How much energy is released when 65.8 g of water freezes?
