Here are the essential concepts you must grasp in order to answer the question correctly.
Quantum Numbers
Quantum numbers are a set of numerical values that describe the unique quantum state of an electron in an atom. The principal quantum number (n) indicates the energy level, while the azimuthal quantum number (l) defines the shape of the orbital. Valid combinations of n and l must satisfy the condition that l can take on integer values from 0 to n-1.
Recommended video:
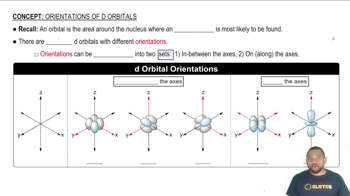
Orbital Types
Orbitals are regions in an atom where there is a high probability of finding electrons. Each type of orbital is designated by a letter: s (l=0), p (l=1), d (l=2), and f (l=3). The type of orbital is determined by the value of the azimuthal quantum number (l), which must be less than the principal quantum number (n) for the orbital to exist.
Recommended video:
Existence of Orbitals
Not all combinations of n and l correspond to real orbitals. For example, while 1s, 2p, and 4s are valid orbitals, 2d is not valid because the azimuthal quantum number l cannot equal 2 when n is 2; it must be less than n. Therefore, understanding the restrictions on quantum numbers is essential for determining which orbitals exist.
Recommended video: