Here are the essential concepts you must grasp in order to answer the question correctly.
Concentration and Molarity
Concentration refers to the amount of solute present in a given volume of solution. Molarity, a common unit of concentration, is defined as moles of solute per liter of solution (mol/L). To calculate molarity from mass percent, one must first determine the mass of solute in a specific volume of solution, which can be derived from the solution's density.
Recommended video:
Acid-Base Equilibria
Acid-base equilibria involve the dissociation of acids and bases in solution, which can be described using equilibrium constants (Ka for acids and Kb for bases). For phosphoric acid (H3PO4), it can lose protons in a stepwise manner, leading to the formation of various species such as H2PO4- and PO43-. Understanding these equilibria is essential for calculating the concentrations of all species in the solution.
Recommended video:
Arrhenius Acids and Bases
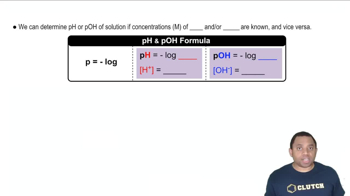
pH and pOH Calculations
pH is a measure of the hydrogen ion concentration in a solution, calculated as pH = -log[H3O+]. The pOH, which measures hydroxide ion concentration, is related to pH by the equation pH + pOH = 14 at 25°C. To find the pH of the solution, one must first determine the concentration of H3O+ ions, which can be derived from the dissociation of H3PO4 and the equilibrium constants provided.
Recommended video: