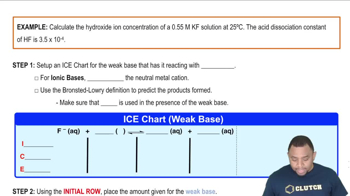
Calculate 3OH-4 for each of the following solutions, and indicate whether the solution is acidic, basic, or neutral: (a) 3H+4 = 0.0505 M
Deuterium oxide 1D2O, where D is deuterium, the hydrogen-2 isotope) has an ion-product constant, Kw, of 8.9 * 10-16 at 20 °C. Calculate 3D+4 and 3OD-4 for pure (neutral) D2O at this temperature.
 Verified step by step guidance
Verified step by step guidance
Verified Solution
Key Concepts
Ion-Product Constant (Kw)

Concentration of Ions in Neutral Solutions
Temperature Effects on Ionization
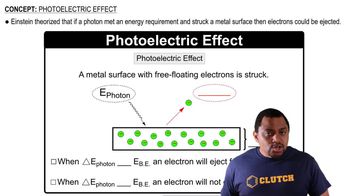
Calculate 3OH-4 for each of the following solutions, and indicate whether the solution is acidic, basic, or neutral: (b) 3H+4 = 2.5 * 10-10 M
Calculate 3OH-4 for each of the following solutions, and indicate whether the solution is acidic, basic, or neutral: (c) a solution in which 3H+4 is 1000 times greater than 3OH-4.
By what factor does 3H+4 change for a pH change of (a) 2.00 units?
The average pH of normal arterial blood is 7.40. At normal body temperature 137 °C2, Kw = 2.4 * 10-14. Calculate 3H+4, 3OH-4, and pOH for blood at this temperature.
Addition of the indicator methyl orange to an unknown solution leads to a yellow color. The addition of bromthymol blue to the same solution also leads to a yellow color. (b) What is the range (in whole numbers) of possible pH values for the solution?
