In a series of experiments, a chemist prepared three different compounds that contain only iodine and fluorine and determined the mass of each element in each compound: Compound Mass of Iodine (g) Mass of Fluorine (g) 1 4.75 3.56 2 7.64 3.43 3 9.41 9.86 (a) Calculate the mass of fluorine per gram of iodine in Compound 3.
"The diameter of a rubidium atom is 495 pm We will consider two different ways of placing the atoms on a surface. In arrangement A, all the atoms are lined up with one another to form a square grid. Arrangement B is called a close-packed arrangement because the atoms sit in the 'depressions' formed by the previous row of atoms:

(c) If extended to three dimensions, which arrangement would lead to a greater density for Rb metal?"

Verified Solution
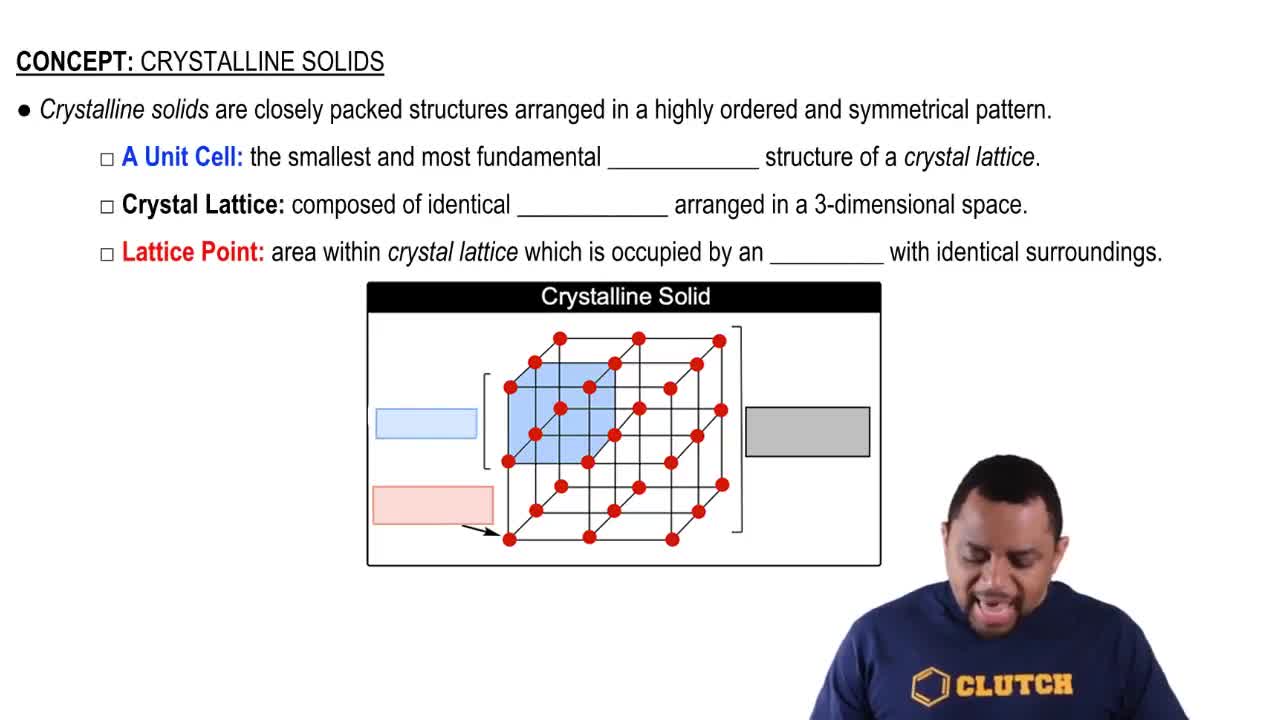
Key Concepts
Atomic Arrangement

Density

Close-Packing
There are two different isotopes of bromine atoms. Under normal conditions, elemental bromine consists of Br2 molecules, and the mass of a Br2 molecule is the sum of the masses of the two atoms in the molecule. The mass spectrum of Br2 consists of three peaks: Mass (u) Relative Size 157.836 0.2569 159.834 0.4999 161.832 0.2431 (a) What is the origin of second (mass of 159.834 amu) peak (of what isotopes does each consist)?
"The diameter of a rubidium atom is 495 pm We will consider two different ways of placing the atoms on a surface. In arrangement A, all the atoms are lined up with one another to form a square grid. Arrangement B is called a close-packed arrangement because the atoms sit in the 'depressions' formed by the previous row of atoms:
(c) By what factor has the number of atoms on the surface increased in going to arrangement B from arrangement A?
(b) Pentane is the alkane with a chain of five carbon atoms. Determine its empirical formula.
Cyclopropane is an interesting hydrocarbon. Instead of having three carbons in a row, the three carbons form a ring, as shown in this perspective drawing (see Figure 2.18 for a prior example of this kind of drawing):
Cyclopropane was at one time used as an anesthetic, but its use was discontinued, in part because it is highly flammable. (a) How does it differ from that of propane?
(b) Pentane is the alkane with a chain of five carbon atoms. Determine its molecular formula.
