"The diameter of a rubidium atom is 495 pm We will consider two different ways of placing the atoms on a surface. In arrangement A, all the atoms are lined up with one another to form a square grid. Arrangement B is called a close-packed arrangement because the atoms sit in the 'depressions' formed by the previous row of atoms:

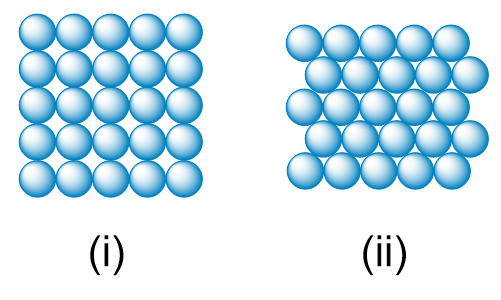
(c) By what factor has the number of atoms on the surface increased in going to arrangement B from arrangement A?

Verified step by step guidance

1. Determine the area occupied by a single atom in arrangement A (square grid). The area of a square is given by the side length squared. Here, the side length is the diameter of the atom.
2. Calculate the area occupied by a single atom in arrangement B (close-packed arrangement). In this arrangement, each atom is surrounded by six others, forming a hexagon. The area of a hexagon can be calculated using the formula: \( \frac{3\sqrt{3}}{2} \times (\text{radius})^2 \).
3. Compare the areas calculated in steps 1 and 2 to determine the relative packing densities of the two arrangements.
4. Calculate the number of atoms per unit area for both arrangements by taking the reciprocal of the area occupied by a single atom in each arrangement.
5. Determine the factor by which the number of atoms on the surface has increased by dividing the number of atoms per unit area in arrangement B by the number of atoms per unit area in arrangement A.

Key Concepts

Atomic Arrangement

Atomic arrangement refers to the spatial organization of atoms in a material. In the context of the question, arrangement A depicts a square grid where atoms are aligned in rows and columns, while arrangement B shows a close-packed structure where atoms occupy the depressions of the previous row, maximizing density and minimizing empty space.

Close-Packing

Close-packing is a method of arranging spheres (or atoms) in a way that maximizes the number of spheres in a given volume. This arrangement is more efficient than a simple grid because it allows for more atoms to fit into the same area, leading to a higher atomic density and potentially greater material strength.

Surface Density

Surface density is a measure of how many atoms are present per unit area on a surface. In comparing arrangements A and B, calculating the surface density will reveal how many more atoms can be accommodated in the close-packed arrangement compared to the square grid, thus allowing for the determination of the factor by which the number of atoms has increased.