At an underwater depth of 100 m, the pressure is 1.106 MPa. What should the partial pressure of oxygen be in the diving gas for the mole fraction of oxygen in the mixture to be 0.21, the same as in air?

Verified step by step guidance

1. Identify the total pressure at the given depth, which is 1.106 MPa.
2. Understand that the mole fraction of oxygen in the mixture is given as 0.21.
3. Use the formula for partial pressure: \( P_{\text{O}_2} = \text{mole fraction of } \text{O}_2 \times \text{total pressure} \).
4. Substitute the given values into the formula: \( P_{\text{O}_2} = 0.21 \times 1.106 \text{ MPa} \).
5. Calculate the partial pressure of oxygen using the substituted values.

Key Concepts

Partial Pressure

Partial pressure refers to the pressure exerted by a single component of a gas mixture. According to Dalton's Law of Partial Pressures, the total pressure of a gas mixture is the sum of the partial pressures of each individual gas. In this context, understanding how to calculate the partial pressure of oxygen based on its mole fraction is essential for determining the appropriate composition of the diving gas.

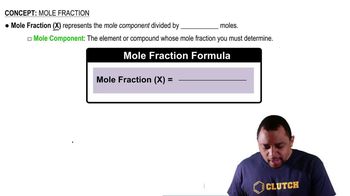
Mole Fraction

Mole fraction is a way of expressing the concentration of a component in a mixture, defined as the ratio of the number of moles of that component to the total number of moles of all components in the mixture. In this question, the mole fraction of oxygen is given as 0.21, indicating that 21% of the gas mixture should be oxygen. This concept is crucial for calculating the partial pressure of oxygen in the diving gas.

Gas Laws

Gas laws describe the behavior of gases under various conditions of pressure, volume, and temperature. The ideal gas law (PV=nRT) is particularly relevant here, as it relates the pressure of a gas to its volume and temperature. Understanding these laws helps in calculating how the pressure at a certain depth affects the partial pressures of gases in a diving scenario.