Density of Geometric Objects - Online Tutor, Practice Problems & Exam Prep

Understanding the relationship between mass, volume, and density is crucial in chemistry. Density is defined as mass divided by volume. This concept extends to geometric shapes such as spheres, cubes, and cylinders, each with its own volume formula. The volume of a sphere is calculated using:

$V=\frac{4\pi r^3}{3}$

where r is the radius. For a cube, the volume is:

$a^3$

with a representing the edge length. A cylinder's volume is found with:

$V=\pi r^{2}h$

incorporating both the radius and the height. These formulas allow us to solve density-related problems by connecting the mass of an object to its geometric volume. Generally, these volume equations are provided by instructors or found on formula sheets, so memorization is not required.

Density of Geometric Objects Concept

So we understand that density is just mass per volume. Now we're going to take that idea of density and apply it to geometric objects. We're going to say here when given the mass of a geometric object, you can relate it to its volume and density. Our typical geometric objects are a sphere, a cube and a cylinder. Each one of them has their own volume equation, which when later on relate to density if we wish.

So here we have a sphere. Now in this sphere we have R radius and remember the radius is just the distance from the center to the edge of the sphere. When it comes to a sphere, its volume equation is V=43πr3. Notice none of these formulas are going to write are in purple boxes, which means you don't need to commit it to memory. Typically when it comes to volumes of geometric objects, your professor will give it to you within the question or on a formula sheet.

Now when it comes to a cube, a cube has all these sides, which we label a. In a cube we assume that they're all of equal length. As a result of this, the volume of a cube is equal to V=a3, where again A is equal to the length or the edge of that cube. Finally, we have a cylinder and in the cylinder we have to take into account 2 variables. We have the height of the cylinder, and we have of course again the radius of the cylinder. Taking these two into perspective, when it comes to a cylinder we have V=πr2h.

So now we're going to take a look at density questions which relate to these different types of geometric objects.

Density of Geometric Objects Example

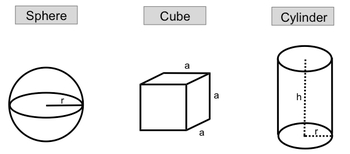
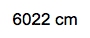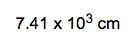So here in this example question, it says the density of silver is 10.5 grams per centimeters cubed. What is the mass in kilograms of a cube of silver that measures .56 meters on each side? All right, although we're talking about density here, and we're talking about a cube, we can still apply the rules that we learn when it comes to given amounts, conversion factors, and end amounts.

So in this question our end amount or given amount actually is the one that has only one unit connected to it and that would be our 0.56 meters. So this is our given amount. Then we have to think about where is our end amount, where do we need to go and where do we stop. Our end amount here would be kilograms, so we need kilograms from the silver cube. Next we look to see what kind of conversion factors are available. Here we have the density of the silver. Remember, density itself is a conversion factor because it's tying together two different units. So that would be 10.51 cm³.

All right, so now let's put it all together. So we have given here given amount. We have to get to end amount and remember to connect them together. We use our conversion factors. Now we see our conversion factor. There is one 10.5g per centimeters cubed. We can try to isolate these grams here. If I can isolate those grams, I can convert them later into kilograms. But to be able to isolate those grams I have to cancel out the centimeters cubed. Remember, centimeters cubed is just a unit for volume. Sometimes we're given an amount. We have our given amount, but sometimes we have to change it up. We have to change it so that we can use it within our dimensional analysis setup.

Since this whole section is on the density of geometric objects and we have a cube, I can determine the volume of the cube. Remember volume equals length cubed, so that would be 0.563 meters cubed, so that comes out to be 0.175616cm³. So this is my actual given amount that I'm going to utilize within this setup. I need to change it to meters cubed because from there I can convert it to centimeters cubed and then from centimeters cubed I'll be able to cancel out the centimeters from the density and be left with grams all right.

So our conversion factor one is just a metric prefix. Conversion meters go here on the bottom, centimeters go here on top. Remember the coefficient of one goes on the same side with the metric prefix SO1 centi is 10-2. Here these meters are cubed, but these are not. So I would have to cube the whole thing. Then we're going to have our meters. Cubes cancel out and now we have centimeters cubed. Because it's in centimeters cubed, I can now use my conversion factor too. So my conversion factor two. I bring this down 10.5g, 11 cm³ on the bottom centimeters cubes will cancel out and now I have grams of my substance, but I don't want it in grams, I need it in kilograms.

So one more conversion factor is actually another metric prefix conversion. So we're going to put here grams on the bottom, kilograms on top. Remember kilo is a metric prefix so 1 K is 103. So grams here cancel out and I'll be left with kilograms at the end. So when you plug this in initially it'll be 0.175616 times 10.5 / 10-2 which is going to be cubed divided by also 103. If you plug this incorrectly, you'll get 1843.968 kilograms. But looking back on the original question, .56 has two sig figs and 10.5 has three sig figs. So we have to go with the least number of significant figures. So getting this to two sick figs, we can write it either as 1800 kilograms or 1.8*103 kilograms. Either one is a reliable, reasonable answer.

So just remember sometimes our dimensional analysis set up the given amount has to be changed a little bit in order to fit and cancel out with other present units. By doing that, we're able to isolate our kilograms within this example. Now that we've done this question, let's move on to our practice question.

A copper wire (density = 8.96 g/cm³) has a diameter of 0.32 mm. If a sample of this copper wire has a mass of 21.7 g, how long is the wire?

• A.
• B.
• C.
• D.
• E.

If the density of a certain spherical atomic nucleus is 1.0 x 10¹⁴ g/cm³ and its mass is 3.5 x 10^-23 g, what is the radius in angstroms? (Å= 10⁻¹⁰ m)

• A.
• B.
• C.
• D.
• E.

Here’s what students ask on this topic:

How do you find the density of a cylinder?

To find the density of a cylinder, you need to know two things: the mass of the cylinder and its volume. Density is defined as mass per unit volume. The formula for density (ρ) is:

$\rho =\frac{\mathrm{mass}}{\mathrm{volume}}$

First, measure the mass of the cylinder using a scale, ensuring you have the mass in kilograms (kg) or grams (g).

Next, calculate the volume of the cylinder. The volume of a cylinder is found using the formula:

$V=\Pi r^{2}h$

where:

• $\Pi$ (pi) is approximately 3.14159
• $r$ is the radius of the base of the cylinder
• $h$ is the height of the cylinder

Make sure to use consistent units when calculating the volume (e.g., if you're using centimeters for the radius and height, the volume will be in cubic centimeters).

Once you have both the mass and the volume, divide the mass by the volume to get the density. Ensure that your final density units are consistent (e.g., grams per cubic centimeter or kilograms per cubic meter).

How do you find the density of a cube?

To find the density of a cube, you'll need to know two key pieces of information: the mass of the cube and its volume. The formula for density (ρ) is:

$\rho =\frac{\mathrm{mass}}{\mathrm{volume}}$

First, measure the mass of the cube using a balance or scale, ensuring you have the mass in grams (g) or kilograms (kg). To calculate the volume of the cube, measure the length of one of its edges, since all edges of a cube are equal. Let's call this measurement 'a'. The volume (V) is then found by cubing this edge length:

$V=a^3$

Once you have both the mass (m) and the volume (V), plug these values into the density formula:

$\rho =\frac{m}{V}$

Make sure your units are consistent (e.g. if mass is in grams, volume should be in cubic centimeters for the density to be in grams per cubic centimeter). Calculate the quotient to find the density, which will give you an understanding of how much mass is contained in a certain volume of the cube.

How do you find the density of a sphere?

To find the density of a sphere, you need to know two key pieces of information: the mass of the sphere and its volume. The formula for density (ρ) is:

$\rho =\frac{\mathrm{mass}}{\mathrm{volume}}$

First, measure the mass of the sphere using a scale. This should be straightforward and is given in units of mass such as grams (g) or kilograms (kg).

Next, calculate the volume of the sphere. The volume (V) of a sphere is calculated using the formula:

$V=\frac{4}{3}\Pi r^3$

Here, 'r' is the radius of the sphere. Measure the diameter of the sphere and divide by two to get the radius. Make sure to use the same unit of measurement for the radius as you will for the volume.

Once you have the volume, divide the mass of the sphere by this volume to get the density. Ensure that your units are consistent when performing these calculations (e.g. if mass is in grams, volume should be in cubic centimeters for the density in g/cm³).

Remember, the density will be a measure of how much mass is contained in a given volume of the sphere.