Textbook Question
What are the possible values of ml for each value of l? a. 0
500
views
 Verified step by step guidance
Verified step by step guidance


What are the possible values of ml for each value of l? a. 0
What are the possible values of ml for each value of l? b. 1
Which set of quantum numbers cannot occur together to specify an orbital? a. n = 2, l = 1, ml = -1 b. n = 3, l = 2, ml = 0 c. n = 3, l = 3, ml = 2 d. n = 4, l = 3, ml = 0
Sketch the 1s and 2p orbitals. How do the 2s and 3p orbitals differ from the 1s and 2p orbitals?
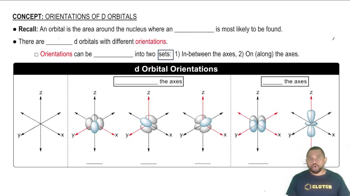
Sketch the 3d orbitals. How do the 4d orbitals differ from the 3d orbitals?