5. Rational Functions
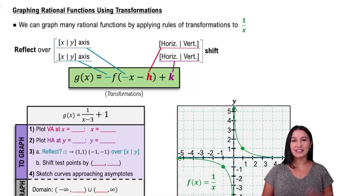
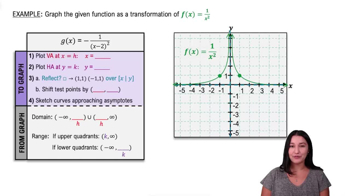
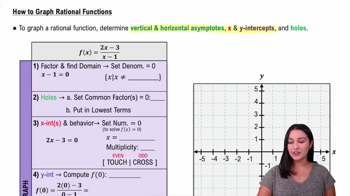
Graphing Rational Functions
5. Rational Functions
Graphing Rational Functions
Practice this topic
- Multiple Choice
Graph the rational function using transformations.
957views - Multiple Choice
Graph the rational function using transformations.
693views1rank - Multiple Choice
Graph the rational function.
1010views1rank - Textbook Question
Graph each rational function. ƒ(x)=[(x-5)(x-2)]/(x2+9)
558views - Textbook Question
Graph each rational function. ƒ(x)=(3x2+3x-6)/(x2-x-12)
559views - Textbook Question
Graph each rational function. See Examples 5–9.
537views - Textbook Question
Graph each rational function. ƒ(x)=(x+2)/(x-3)
553views