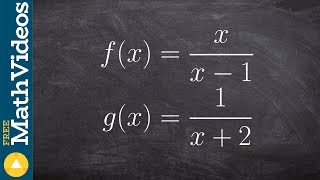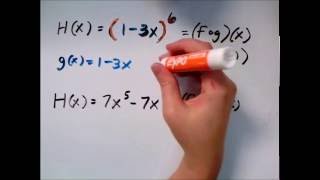3. Functions
Function Composition
3. Functions
Function Composition
Additional 2 creators.
Learn with other creators
Showing 5 of 5 videos
Practice this topic
Textbook Question
Use the graphs of f and g to solve Exercises 83–90.
Find the domain of ƒ/g.
228
views
Textbook Question
Determine whether each function graphed or defined is one-to-one. y = 2x - 8
47
views
Showing 169 of 169 practice