Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Inverse Trigonometric Functions
Problem 3.10.65a
Textbook Question
62–65. {Use of Tech} Graphing f and f'
a. Graph f with a graphing utility.
f(x)=e^−x tan^−1 x on [0,∞)
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the function f(x) = e^(-x) * tan^(-1)(x). This function is a product of the exponential function e^(-x) and the inverse tangent function tan^(-1)(x).
Step 2: Use a graphing utility or software that supports graphing, such as Desmos, GeoGebra, or a graphing calculator, to input the function f(x) = e^(-x) * tan^(-1)(x).
Step 3: Set the domain for the graph. Since the problem specifies the interval [0, ∞), ensure that the graphing utility is set to display the graph starting from x = 0 and extending towards positive infinity.
Step 4: Observe the behavior of the graph. Note how the exponential decay of e^(-x) affects the overall shape of the graph, and how the inverse tangent function, which approaches π/2 as x approaches infinity, influences the graph.
Step 5: Analyze the graph for key features such as intercepts, asymptotic behavior, and any points of interest. This will help in understanding the overall behavior of the function on the given interval.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Exponential Functions
Exponential functions are mathematical expressions in the form f(x) = a * e^(bx), where 'e' is Euler's number (approximately 2.718). In the given function f(x) = e^(-x) * tan^(-1)(x), the term e^(-x) represents a decaying exponential function, which approaches zero as x increases. Understanding the behavior of exponential functions is crucial for analyzing the overall shape and limits of the graph.
Recommended video:

Exponential Functions
Inverse Tangent Function
The inverse tangent function, denoted as tan^(-1)(x) or arctan(x), is the function that returns the angle whose tangent is x. It has a range of (-π/2, π/2) and approaches these limits as x approaches ±∞. In the context of the function f(x) = e^(-x) * tan^(-1)(x), this function influences the growth of f(x) as x increases, particularly since tan^(-1)(x) approaches π/2.
Recommended video:
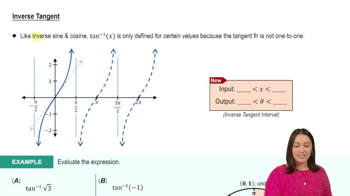
Inverse Tangent
Graphing Utilities
Graphing utilities are software or tools that allow users to visualize mathematical functions and their derivatives. They can plot complex functions, helping to analyze their behavior over specified intervals. For the function f(x) = e^(-x) * tan^(-1)(x) on the interval [0, ∞), using a graphing utility will provide insights into the function's growth, decay, and asymptotic behavior, which is essential for understanding its overall characteristics.
Recommended video:

Graphing The Derivative
Related Videos
Related Practice