Find the area of each triangle ABC.
A = 59.80°, b = 15.00 cm, C = 53.10°
 Verified step by step guidance
Verified step by step guidance
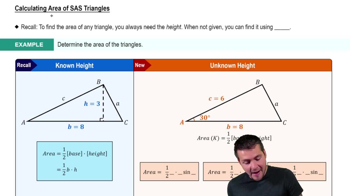


Find the area of each triangle ABC.
A = 59.80°, b = 15.00 cm, C = 53.10°
A plane is headed due south with an airspeed of 192 mph. A wind from a direction of 78.0° is blowing at 23.0 mph. Find the ground speed and resulting bearing of the plane.
A painter is going to apply paint to a triangular metal plate on a new building. Two sides measure 16.1 m and 15.2 m, and the angle between the sides is 125°. What is the area of the surface to be painted?
Find the angle between each pair of vectors. Round to two decimal places as necessary.
〈1, 6〉, 〈-1, 7〉
Find the angle between each pair of vectors. Round to two decimal places as necessary.
3i + 4j, j
Find the exact area of each triangle using the formula 𝓐 = ½ bh, and then verify that Heron's formula gives the same result.
<IMAGE>