Find the angle between each pair of vectors. Round to two decimal places as necessary.
〈4, 0〉, 〈2, 2〉
 Verified step by step guidance
Verified step by step guidance


Find the angle between each pair of vectors. Round to two decimal places as necessary.
〈4, 0〉, 〈2, 2〉
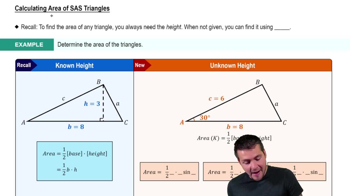
Find the area of each triangle ABC.
A = 59.80°, b = 15.00 cm, C = 53.10°
A plane is headed due south with an airspeed of 192 mph. A wind from a direction of 78.0° is blowing at 23.0 mph. Find the ground speed and resulting bearing of the plane.
A real estate agent wants to find the area of a triangular lot. A surveyor takes measurements and finds that two sides are 52.1 m and 21.3 m, and the angle between them is 42.2°. What is the area of the triangular lot?
Find the angle between each pair of vectors. Round to two decimal places as necessary.
〈1, 6〉, 〈-1, 7〉
Find the angle between each pair of vectors. Round to two decimal places as necessary.
3i + 4j, j