Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
3. Unit Circle
Reference Angles
Problem 72
Textbook Question
Textbook QuestionIn Exercises 61–86, use reference angles to find the exact value of each expression. Do not use a calculator. tan 9𝜋 2
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
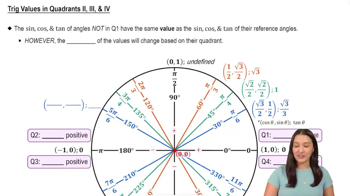
Reference Angles
A reference angle is the acute angle formed by the terminal side of an angle in standard position and the x-axis. It is always measured as a positive angle and is used to simplify the calculation of trigonometric functions. For angles greater than 360 degrees or less than 0 degrees, the reference angle can be found by subtracting or adding full rotations (360 degrees or 2π radians) until the angle falls within the first rotation.
Recommended video:

Reference Angles on the Unit Circle
Tangent Function
The tangent function, denoted as tan(θ), is defined as the ratio of the opposite side to the adjacent side in a right triangle. In the unit circle, it can also be expressed as the ratio of the sine and cosine functions: tan(θ) = sin(θ)/cos(θ). Understanding the behavior of the tangent function in different quadrants is essential for evaluating its values based on the reference angle.
Recommended video:

Introduction to Tangent Graph
Quadrants and Angle Measurement
The coordinate plane is divided into four quadrants, each corresponding to specific ranges of angle measurements. Angles are measured in radians, with 0 radians at the positive x-axis, π/2 radians at the positive y-axis, π radians at the negative x-axis, and 3π/2 radians at the negative y-axis. Knowing the quadrant in which an angle lies helps determine the sign of the trigonometric functions, which is crucial for finding the exact value of expressions like tan(9π/2).
Recommended video:

Quadratic Formula

 5:31m
5:31mWatch next
Master Reference Angles on the Unit Circle with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice