Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
4. Graphing Trigonometric Functions
Graphs of Tangent and Cotangent Functions
Problem 4.15c
Textbook Question
For each function, give the amplitude, period, vertical translation, and phase shift, as applicable.
y = 1/3 tan (3x - π/3)
 Verified step by step guidance
Verified step by step guidance1
Identify the general form of the tangent function: \( y = a \tan(bx - c) + d \).
Determine the amplitude: For tangent functions, amplitude is not defined as they have no maximum or minimum values.
Calculate the period: The period of \( \tan(bx) \) is \( \frac{\pi}{b} \). Here, \( b = 3 \), so the period is \( \frac{\pi}{3} \).
Find the phase shift: The phase shift is given by \( \frac{c}{b} \). Here, \( c = \frac{\pi}{3} \) and \( b = 3 \), so the phase shift is \( \frac{\pi/3}{3} = \frac{\pi}{9} \).
Determine the vertical translation: The vertical translation is given by \( d \). In this function, \( d = 0 \), so there is no vertical translation.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Amplitude
In trigonometric functions, amplitude refers to the height of the wave from its midline to its peak. However, for the tangent function, amplitude is not defined as it does not have a maximum or minimum value; it extends infinitely in both directions. Instead, we focus on the vertical stretch or compression, which is determined by the coefficient in front of the function.
Recommended video:
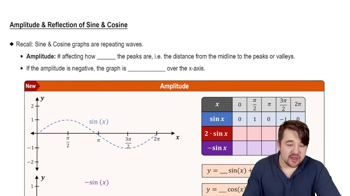
Amplitude and Reflection of Sine and Cosine
Period
The period of a trigonometric function is the length of one complete cycle of the wave. For the tangent function, the period is calculated using the formula π divided by the coefficient of x in the argument. In this case, with a coefficient of 3, the period is π/3, indicating that the function repeats every π/3 units along the x-axis.
Recommended video:

Period of Sine and Cosine Functions
Phase Shift
Phase shift refers to the horizontal displacement of a trigonometric function from its standard position. It is determined by the horizontal translation in the function's argument. For the function y = (1/3) tan(3x - π/3), the phase shift can be found by setting the inside of the tangent function equal to zero, leading to a shift of π/9 units to the right.
Recommended video:
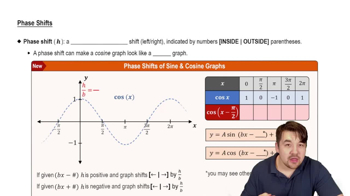
Phase Shifts

 5:43m
5:43mWatch next
Master Introduction to Tangent Graph with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice














