In Exercises 33–38, find the area of the triangle having the given measurements. Round to the nearest square unit.C = 102°, a = 16 meters, b = 20 meters

Verified step by step guidance

1. Identify the formula for the area of a triangle using two sides and the included angle: \( \text{Area} = \frac{1}{2}ab\sin(C) \).
2. Substitute the given values into the formula: \( a = 16 \), \( b = 20 \), and \( C = 102^\circ \).
3. Calculate \( \sin(102^\circ) \) using a calculator or trigonometric table.
4. Multiply the values: \( \frac{1}{2} \times 16 \times 20 \times \sin(102^\circ) \).
5. Round the result to the nearest square unit to find the area of the triangle.

Key Concepts

Law of Cosines

The Law of Cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. It is particularly useful for finding the length of a side when two sides and the included angle are known. The formula is c² = a² + b² - 2ab * cos(C), where C is the angle opposite side c. This concept is essential for solving triangles that are not right-angled.

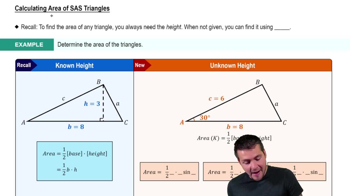
Area of a Triangle

The area of a triangle can be calculated using the formula A = 1/2 * a * b * sin(C), where a and b are the lengths of two sides and C is the included angle. This formula is derived from the basic definition of area and is particularly useful when two sides and the included angle are known, as in this problem. Understanding this formula is crucial for finding the area of non-right triangles.

Trigonometric Functions

Trigonometric functions, such as sine, cosine, and tangent, relate the angles of a triangle to the ratios of its sides. In this context, the sine function is particularly important for calculating the area of a triangle when given two sides and the included angle. Familiarity with these functions allows for the effective application of trigonometric identities and formulas in solving various problems in trigonometry.