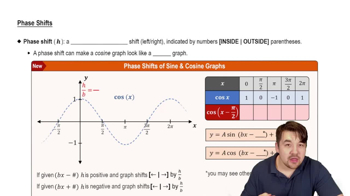
Fill in the blank(s) to correctly complete each sentence.
The graph of y = 6 + 3 sin x is obtained by shifting the graph of y = 3 sin x ________ unit(s) __________ (up/down).
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: