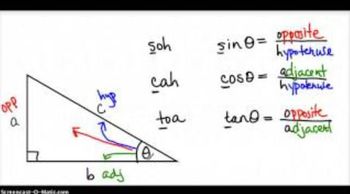
Use the appropriate reciprocal identity to find each function value. Rationalize denominators when applicable. See Example 1. csc θ , given that sin θ = ―3/7

Key Concepts

Reciprocal Identities

Reciprocal identities in trigonometry relate the primary trigonometric functions to their reciprocals. For instance, the cosecant function (csc) is the reciprocal of the sine function (sin), meaning csc θ = 1/sin θ. Understanding these identities is crucial for solving problems that require finding one function value based on another.

Rationalizing Denominators

Rationalizing the denominator is a process used to eliminate any radical expressions from the denominator of a fraction. This is often done by multiplying the numerator and denominator by a suitable value that will simplify the expression. In trigonometry, this is important for presenting answers in a standard form, especially when dealing with functions that may involve square roots.

Sine Function and Its Values

The sine function is a fundamental trigonometric function that relates the angle of a right triangle to the ratio of the length of the opposite side to the hypotenuse. In this case, knowing that sin θ = -3/7 allows us to find csc θ using the reciprocal identity. Understanding the sine function's properties and its range is essential for interpreting and solving trigonometric equations.