Here are the essential concepts you must grasp in order to answer the question correctly.
Rayleigh's Criterion
Rayleigh's criterion is a formula used to determine the minimum angular resolution of an optical system, such as a telescope or antenna. It states that two point sources are resolvable when the central maximum of one diffraction pattern coincides with the first minimum of another. This criterion is crucial for understanding how closely spaced objects can be distinguished based on the wavelength of the signal and the diameter of the receiving dish.
Diffraction Limit
The diffraction limit refers to the fundamental limit on the resolution of an imaging system due to the wave nature of light or other electromagnetic waves. It is influenced by the wavelength of the signal and the aperture size of the receiving dish. A larger dish can collect more waves and reduce the effects of diffraction, allowing for better resolution of closely spaced signals.
Recommended video:
Antenna Diameter and Wavelength Relationship
The relationship between the diameter of an antenna (or receiving dish) and the wavelength of the signal is critical for determining resolution. According to the formula derived from Rayleigh's criterion, the minimum diameter required to resolve two signals is proportional to the wavelength of the signal and inversely proportional to the angular separation of the sources. This relationship helps in calculating the necessary size of the receiving dish to achieve the desired resolution.
Recommended video:
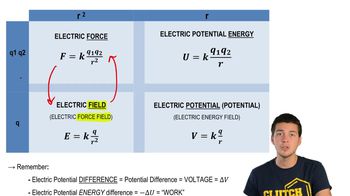
Relationships Between Force, Field, Energy, Potential