Here are the essential concepts you must grasp in order to answer the question correctly.
Faraday's Law of Electromagnetic Induction
Faraday's Law states that the induced electromotive force (emf) in a closed loop is directly proportional to the rate of change of magnetic flux through the loop. This principle is fundamental in understanding how changing magnetic fields can generate electric currents. In this scenario, as the circumference of the loop decreases, the area enclosed by the loop also changes, leading to a change in magnetic flux and thus inducing an emf.
Recommended video:
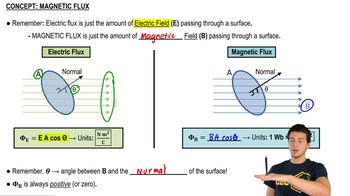
Magnetic Flux
Magnetic flux is defined as the product of the magnetic field strength and the area through which the field lines pass, taking into account the angle between the field lines and the normal to the surface. It is measured in webers (Wb). In this problem, the magnetic flux through the loop will decrease as the area of the loop decreases due to the shrinking circumference, which is crucial for calculating the induced emf.
Recommended video:
Rate of Change of Circumference
The rate of change of circumference refers to how quickly the circumference of the loop is decreasing, which in this case is given as 12.0 cm/s. This rate directly affects the change in area of the loop over time, influencing the rate of change of magnetic flux. Understanding this rate is essential for applying Faraday's Law to find the induced emf at a specific time.
Recommended video:
Circumference, Period, and Frequency in UCM