Polystyrene has dielectric constant 2.6 and dielectric strength 2.0x10^7 V/m. A piece of polystyrene is used as a dielectric in a parallel-plate capacitor, filling the volume between the plates. (a) When the electric field between the plates is 80% of the dielectric strength, what is the energy density of the stored? (b) When the capacitor is connected to a battery with voltage 500.0 V, the electric field between the plates is 80% of the dielectric strength. What is the area of each plate if the capacitor stores 0.200 mJ of energy under these conditions?

Verified step by step guidance

1. Step 1: Calculate the electric field (E) when it is 80% of the dielectric strength. Use the formula E = 0.8 \times \text{dielectric strength}.
2. Step 2: Use the formula for energy density (u) of a capacitor with a dielectric, which is u = \frac{1}{2} \epsilon_0 \kappa E^2, where \epsilon_0 is the permittivity of free space (8.85 \times 10^{-12} F/m) and \kappa is the dielectric constant.
3. Step 3: For part (b), calculate the electric field (E) again using the same method as in Step 1 since the conditions are the same.
4. Step 4: Use the formula for the capacitance of a parallel-plate capacitor with a dielectric, C = \kappa \epsilon_0 \frac{A}{d}, where A is the area of the plates and d is the separation between them. Solve for A using the relationship between capacitance, stored energy (U), and voltage (V): U = \frac{1}{2} C V^2.
5. Step 5: Rearrange the formula from Step 4 to solve for the area (A) of each plate, using the given values for the stored energy, voltage, and calculated capacitance.

Key Concepts

Dielectric Constant

The dielectric constant, also known as relative permittivity, is a measure of a material's ability to store electrical energy in an electric field. It is defined as the ratio of the capacitance of a capacitor with the dielectric material to the capacitance of the same capacitor in a vacuum. A higher dielectric constant indicates a greater ability to store charge, which is crucial for understanding how materials affect the performance of capacitors.

Energy Density in a Capacitor

Energy density in a capacitor refers to the amount of energy stored per unit volume of the dielectric material. It can be calculated using the formula U = 1/2 ε E², where U is the energy density, ε is the permittivity of the dielectric, and E is the electric field strength. This concept is essential for determining how much energy can be stored in a capacitor under specific electric field conditions.

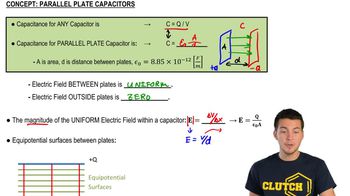
Capacitance and Plate Area

The capacitance of a parallel-plate capacitor is directly related to the area of the plates and the distance between them, described by the formula C = ε(A/d), where C is capacitance, A is the area of the plates, d is the separation, and ε is the permittivity of the dielectric. Understanding this relationship is vital for calculating the required plate area when given energy storage and voltage conditions, as it allows for the design of capacitors to meet specific energy requirements.