A Carnot refrigerator is operated between two heat reservoirs at temperatures of 320 K and 270 K. (c) What is the coefficient of performance of the refrigerator?

Verified step by step guidance

1. Identify the temperatures of the hot and cold reservoirs. Here, the hot reservoir temperature (Th) is 320 K and the cold reservoir temperature (Tc) is 270 K.
2. Recall the formula for the coefficient of performance (COP) of a Carnot refrigerator, which is given by \(COP = \frac{T_c}{T_h - T_c}\).
3. Substitute the values of Th and Tc into the formula. So, plug in Th = 320 K and Tc = 270 K into the formula.
4. Perform the subtraction in the denominator of the formula to find \(T_h - T_c\).
5. Calculate the division \(\frac{T_c}{T_h - T_c}\) to find the coefficient of performance of the refrigerator.

Key Concepts

Carnot Cycle

The Carnot cycle is a theoretical thermodynamic cycle that provides the maximum possible efficiency for a heat engine or refrigerator operating between two temperature reservoirs. It consists of four reversible processes: two isothermal and two adiabatic. The efficiency of any real engine or refrigerator cannot exceed that of a Carnot cycle operating between the same temperatures.

Coefficient of Performance (COP)

The Coefficient of Performance (COP) is a measure of the efficiency of a refrigerator or heat pump, defined as the ratio of the heat removed from the cold reservoir to the work input required to remove that heat. For a Carnot refrigerator, the COP can be calculated using the formula COP = T_c / (T_h - T_c), where T_c is the absolute temperature of the cold reservoir and T_h is the absolute temperature of the hot reservoir.

Thermodynamic Temperature Scale

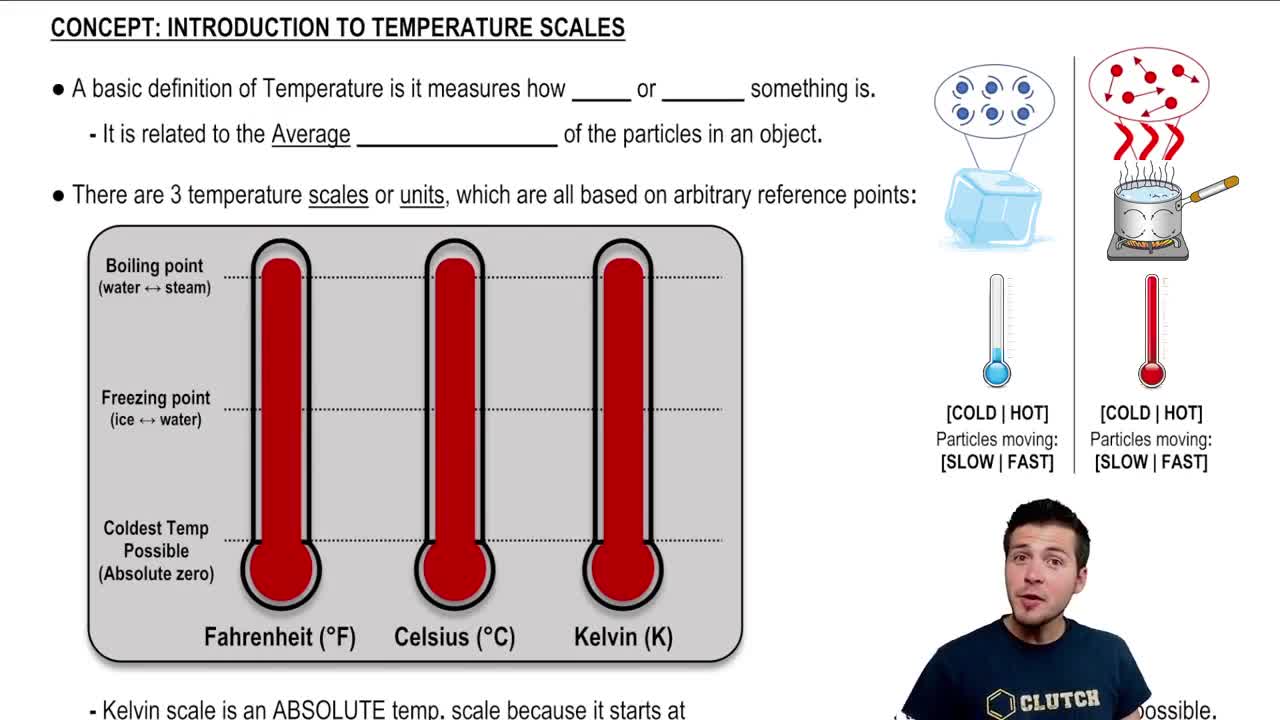
The thermodynamic temperature scale is an absolute temperature scale based on the principles of thermodynamics, measured in Kelvin (K). It is crucial for calculations in thermodynamics because it avoids negative values and provides a direct relationship between temperature and energy. In the context of the Carnot refrigerator, temperatures of the heat reservoirs must be expressed in Kelvin to accurately determine the COP.