A cylinder contains 0.100 mol of an ideal monatomic gas. Initially the gas is at 1.00 * 10^5 Pa and occupies a volume of 2.50 * 10^-3 m^3. (b) If the gas is allowed to expand to twice the initial volume, find the final temperature (in kelvins) and pressure of the gas if the expansion is (i) isothermal; (ii) isobaric; (iii) adiabatic.

Verified step by step guidance

1. Identify the initial conditions of the gas: number of moles (n = 0.100 mol), initial pressure (P1 = 1.00 * 10^5 Pa), and initial volume (V1 = 2.50 * 10^-3 m^3).
2. Calculate the initial temperature (T1) using the ideal gas law, PV = nRT, where R is the ideal gas constant (8.314 J/(mol*K)).
3. For isothermal expansion (i), use the fact that temperature remains constant (T2 = T1). Apply the ideal gas law to find the final pressure (P2) after the volume has doubled (V2 = 2 * V1).
4. For isobaric expansion (ii), the pressure remains constant (P2 = P1). Calculate the final temperature (T2) using the relation from the ideal gas law, considering the volume has doubled (V2 = 2 * V1).
5. For adiabatic expansion (iii), use the adiabatic condition where PV^gamma = constant (gamma = 5/3 for monatomic gas). Calculate the final temperature (T2) and pressure (P2) using the relations T2 = T1 * (V1/V2)^(gamma-1) and P2 = P1 * (V1/V2)^gamma.

Key Concepts

Ideal Gas Law

The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of an ideal gas through the equation PV = nRT. Here, P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is temperature in kelvins. This law is fundamental for understanding how changes in one property affect the others in gas behavior.

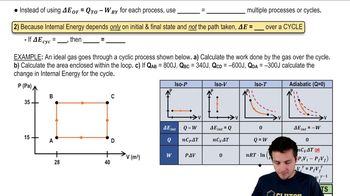
Types of Thermodynamic Processes

Thermodynamic processes can be classified into isothermal (constant temperature), isobaric (constant pressure), and adiabatic (no heat exchange). Each process has distinct characteristics that affect how a gas behaves when it expands or contracts. Understanding these processes is crucial for calculating changes in temperature and pressure during gas expansion.

Monatomic Ideal Gas Properties

Monatomic ideal gases, such as helium or neon, consist of single atoms and exhibit specific heat capacities that differ from diatomic or polyatomic gases. For monatomic gases, the molar specific heat at constant volume (Cv) is 3/2 R, and at constant pressure (Cp) is 5/2 R. These properties are essential for determining temperature changes during various thermodynamic processes.