A metal bar is in the xy-plane with one end of the bar at the origin. A force F = 97.00 N)i + (-3.00 N)j is applied to the bar at the point x = 3.00 m, y = 4.00 m. (b) What are the magnitude and direction of the torque with respect to the origin produced by F?

Verified step by step guidance

1. Identify the position vector \( \vec{r} \) from the origin to the point where the force is applied. In this case, \( \vec{r} = 3.00 \, \text{m} \, \hat{i} + 4.00 \, \text{m} \, \hat{j} \).
2. Write down the force vector \( \vec{F} \) given in the problem. Here, \( \vec{F} = 97.00 \, \text{N} \, \hat{i} - 3.00 \, \text{N} \, \hat{j} \).
3. Use the cross product formula to calculate the torque \( \vec{\tau} \) with respect to the origin. The torque is given by \( \vec{\tau} = \vec{r} \times \vec{F} \).
4. Calculate the components of the torque using the determinant of a matrix formed by the unit vectors \( \hat{i}, \hat{j}, \hat{k} \), and the components of \( \vec{r} \) and \( \vec{F} \).
5. Find the magnitude of the torque vector \( \vec{\tau} \) using the formula \( |\vec{\tau}| = \sqrt{\tau_x^2 + \tau_y^2 + \tau_z^2} \) and determine the direction from the sign of the components.

Key Concepts

Torque

Torque is a measure of the rotational force applied to an object, calculated as the cross product of the position vector and the force vector. It determines how effectively a force can cause an object to rotate about a pivot point. The magnitude of torque depends on the distance from the pivot to the point of force application and the angle at which the force is applied.

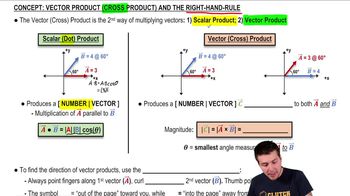
Cross Product

The cross product is a mathematical operation that takes two vectors and produces a third vector that is perpendicular to the plane formed by the original vectors. In the context of torque, the cross product of the position vector (from the pivot to the point of force application) and the force vector gives the torque vector, which indicates both the magnitude and direction of the torque.

Magnitude and Direction of Vectors

In physics, the magnitude of a vector represents its size or strength, while the direction indicates where it points in space. For torque, the magnitude can be calculated using the formula |τ| = rF sin(θ), where r is the distance from the pivot to the point of force application, F is the force applied, and θ is the angle between the position and force vectors. The direction of the torque vector follows the right-hand rule, indicating the axis of rotation.