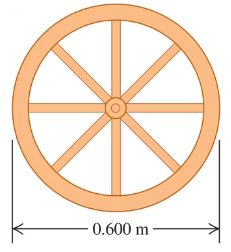
A wagon wheel is constructed as shown in Fig. E9.33. The radius of the wheel is 0.300 m, and the rim has mass 1.40 kg. Each of the eight spokes that lie along a diameter and are 0.300 m long has mass 0.280 kg. What is the moment of inertia of the wheel about an axis through its center and perpendicular to the plane of the wheel? (Use Table 9.2.)

Question

Diagram of a wagon wheel showing rim, spokes, and hub for moment of inertia calculation.

Accepted Answer

Hey, everyone in this problem, a bicycle wheel is made with a RIM and six thin rots. The wheel is placed along a horizontal plane and is mounted on a fixed frictionless vertical axis passing through the wheel's hub. The Rim's diameter is 58 cm and its mass is 1.25 kg. The rim is connected to the hub by the rots. As shown in the figure, The mass of a rod is 0.1 kg and its length is 29 cm. We're asked to calculate the moment of inertia about the vertical axle. Now, we're given this diagram, we have our bicycle wheel, then we have the rim, we have six thin rods pointing from the rim to the center and at the center, we have the hub where our axle is going to pass through. Now, we're asked to calculate the moment of inertia. So the moment of inertia eye on this case, we have to worry about the rots and we have to worry about the rim. They're both going to contribute to the moment of inertia. And so we have the moment of inertia is going to be equal to the moment of inertia of the rods. What's the moment of inertia of the rim? Now, we have six rots, ok. Each of them is gonna have the same moment of inertia. So we're gonna have six multiplied by the moment of inertia of a rod. Ok. And each of these rods, ok. The axle is passing through the end of the rod. So if we look either in the table in our textbook or that your professor provided, and you're looking for a moment of inertia, we have a rod like a thin cylinder, ok? Where it's rotating about the end, we get that the moment of inertia is going to be the mass M and it's the mass of the rod multiplied by the length little L squared divided by three. Yeah, we're gonna add the moment of inertia of the rim. The rim is like a hoop. And so that's gonna be M the mass of the rim multiplied by R the radius of the rim squared. Now, we can simplify this first term. We have six divided by three. And so we can write this as two times the mass of the rod multiplied by the length of the rod squared. What's the mass of the rim multiplied by the radius of the rim squared? Now, we can substitute in the values we have, we're given the maps, we're given the length of the rods, we're given the radius of the rim or the diameter which we can calculate the radius from. So we have everything we need, we just need to substitute in those values. So we get two multiplied by the mass, 0.1 kilograms, multiplied the by the length of the rock. No, the rod length is given in centimeters. We're gonna do a quick conversion. So the length is equal to 29 cm. We want to convert this into our standard unit of meters. So we can multiply and in every one m, There are 100 cm is the unit of centimeter, cancels. What we're effectively doing is taking our centimeters 29 dividing by 100. And we get that the length is 0.29 m. HM. So we have 0.29 m squared in our moment of inertia equation. Now we're gonna add The max of the Rim We're told is 1.2, 5 kg multiplied by the radius of the rim. Now, the radius of the rim is going to be half the diameter, the diameter of the rim Is 58 cm. Ok? So the radius is equal to half of the diameter, 59 cm divided by two, sorry 58 cm divided by two, which gives us a radius cm, which makes sense. OK. These rods go from the Rim right to the center. So it makes sense that they have the same length as the radius of the bike. Ok. So the radius of the bike is 29 centimeters. We've already converted 2029 centimeters into meters. And so for the radius of the rim, we're also multiplying by 0.29 m and this is squared. Hey, if we work this out on our calculator for the first part, we get that the moment of inertia of the rots is 0.01 kilogram meter squared Plus the moment of inertia for the Rim, which is 0. 125. And again, kilogram meter squared can add these together and we get the moment of inertia is 0. kilogram meter squared. The answer choices are rounded to three significant digits. So if we round our answer to three significant digits, this gives us 0.122 kg meter squared. That is a moment of inertia of that bike wheel and that corresponds with answer choice. A thanks everyone for watching. I hope this video helped see you in the next one.

Verified Solution

Key Concepts

Moment of Inertia

Parallel Axis Theorem

Composite Bodies