Here are the essential concepts you must grasp in order to answer the question correctly.
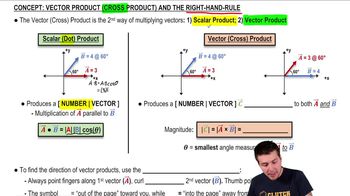
Vector Product (Cross Product)
The vector product, also known as the cross product, of two vectors results in a third vector that is perpendicular to the plane formed by the original vectors. It is calculated using the determinant of a matrix formed by the unit vectors i, j, k and the components of the two vectors. The direction of the resulting vector follows the right-hand rule, and its magnitude is given by the formula |A x B| = |A||B|sin(θ), where θ is the angle between the two vectors.
Recommended video:
Vector (Cross) Product and the Right-Hand-Rule
Unit Vectors
Unit vectors are vectors with a magnitude of one, used to indicate direction. In three-dimensional space, the standard unit vectors are i, j, and k, which represent the x, y, and z axes, respectively. When expressing vectors in terms of unit vectors, each vector can be decomposed into its components along these axes, facilitating operations like addition, subtraction, and the vector product.
Recommended video:
Magnitude of a Vector
The magnitude of a vector is a measure of its length and is calculated using the Pythagorean theorem. For a vector expressed in component form as A = ai + bj + ck, the magnitude is given by |A| = √(a² + b² + c²). In the context of the vector product, the magnitude of the resulting vector indicates the area of the parallelogram formed by the two original vectors, providing insight into their relative orientation and size.
Recommended video:
Calculating Magnitude & Components of a Vector
 Verified step by step guidance
Verified step by step guidance