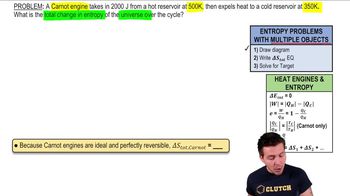
Textbook Question
A car's internal combustion engine can be modeled as a heat engine operating between a combustion temperature of 1500℃ and an air temperature of 20℃ with 30% of the Carnot efficiency. The heat of combustion of gasoline is 47 kJ/g. What mass of gasoline is burned to accelerate a 1500 kg car from rest to a speed of 30 m/s?
573
views