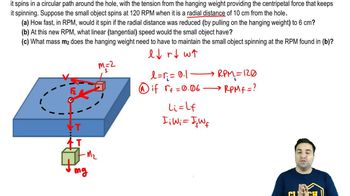
Here are the essential concepts you must grasp in order to answer the question correctly.
Frequency and Wavelength
Frequency is the number of oscillations or cycles that occur in a unit of time, measured in Hertz (Hz). In the context of a vibrating string, the frequency is related to the wavelength and the speed of the wave on the string. The fundamental frequency of a string is determined by its length, tension, and mass per unit length.
Recommended video:
Circumference, Period, and Frequency in UCM
Tension in a String
Tension is the force exerted along the length of a string, which affects its vibration and frequency. The relationship between tension, mass per unit length, and frequency is described by the formula: f = (1/2L)√(T/μ), where f is frequency, L is the length of the vibrating section, T is tension, and μ is mass per unit length. Adjusting the tension alters the frequency of the vibrating string.
Recommended video:
Energy & Power of Waves on Strings
Mass per Unit Length
Mass per unit length (μ) is a measure of how much mass is distributed along a given length of the string, calculated as μ = m/L, where m is the mass and L is the length. This property is crucial for determining the wave speed on the string and influences the frequency of the sound produced. In this case, the mass of the string and its vibrating length are essential for calculating the required tension.
Recommended video:
Spinning on a string of variable length