a. When the displacement of a mass on a spring is ½A, what fraction of the energy is kinetic energy and what fraction is potential energy?

Verified step by step guidance

1. Identify that the total energy (E) in a simple harmonic oscillator like a mass-spring system is conserved and is the sum of kinetic energy (KE) and potential energy (PE).
2. Recognize that the potential energy in a spring system is given by PE = \(\frac{1}{2} k x^2\), where \(k\) is the spring constant and \(x\) is the displacement from the equilibrium position.
3. Understand that at maximum displacement (amplitude A), all the energy is potential, and at the equilibrium position (displacement = 0), all the energy is kinetic. The total mechanical energy is \(E = \frac{1}{2} k A^2\).
4. Calculate the potential energy at the displacement \(x = \frac{1}{2}A\) using the formula for potential energy. Substitute \(x = \frac{1}{2}A\) into the potential energy formula to find \(PE = \frac{1}{2} k (\frac{1}{2}A)^2\).
5. Determine the kinetic energy at \(x = \frac{1}{2}A\) by subtracting the potential energy at this point from the total energy. Use the equation \(KE = E - PE\) to find the kinetic energy.

Key Concepts

Hooke's Law

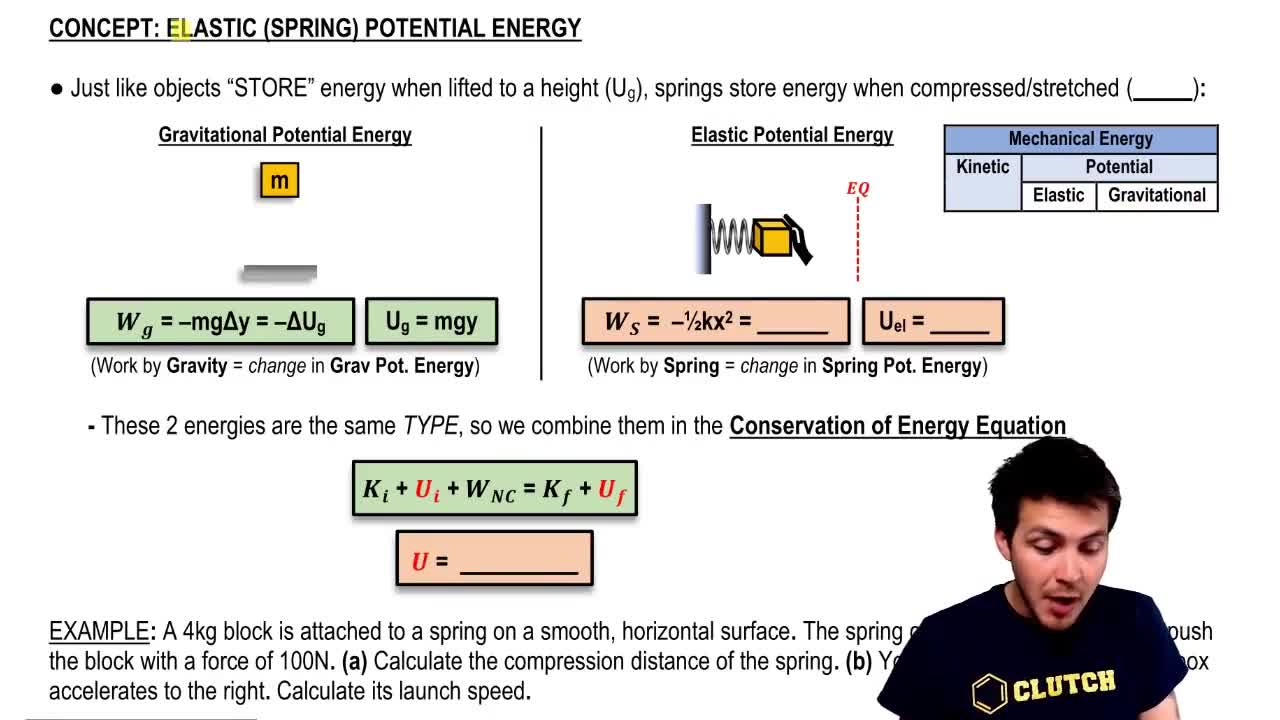
Hooke's Law states that the force exerted by a spring is directly proportional to its displacement from the equilibrium position, expressed as F = -kx, where k is the spring constant. This principle is fundamental in understanding how springs store potential energy when displaced from their rest position.

Potential Energy in Springs

The potential energy (PE) stored in a spring is given by the formula PE = 1/2 kx², where x is the displacement from the equilibrium position. This energy is maximum when the spring is fully compressed or stretched and decreases as the spring returns to its equilibrium position, converting potential energy into kinetic energy.

Kinetic Energy

Kinetic energy (KE) is the energy of an object due to its motion, calculated using the formula KE = 1/2 mv², where m is mass and v is velocity. In the context of a mass on a spring, as the mass moves through the equilibrium position, its potential energy is converted into kinetic energy, reaching maximum kinetic energy when the displacement is zero.