Here are the essential concepts you must grasp in order to answer the question correctly.
Potential Energy
Potential energy is the energy stored in an object due to its position in a force field, such as gravitational or elastic fields. In this context, the potential energy U is defined as a function of position x, incorporating both a quadratic term (Ax²) and a sinusoidal term (B sin(πx/L)). Understanding how potential energy varies with position is crucial for analyzing the forces acting on the particle.
Recommended video:
Force and Potential Energy Relationship
The force acting on a particle can be derived from the potential energy function using the relationship F = -dU/dx. This means that the force is equal to the negative gradient of the potential energy with respect to position. This concept is essential for determining the force at specific positions along the x-axis, as it allows us to calculate how the potential energy changes and thus the corresponding force acting on the particle.
Recommended video:
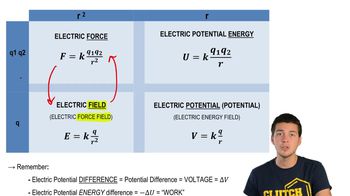
Relationships Between Force, Field, Energy, Potential
Differentiation
Differentiation is a fundamental mathematical operation used to find the rate at which a function changes. In the context of this problem, we need to differentiate the potential energy function U with respect to x to find the force. Mastery of differentiation techniques, including the product and chain rules, is necessary to accurately compute the force at the specified positions (x=0, x=L/2, and x=L).
Recommended video:
Gravitational Force from a Solid Disk