Here are the essential concepts you must grasp in order to answer the question correctly.
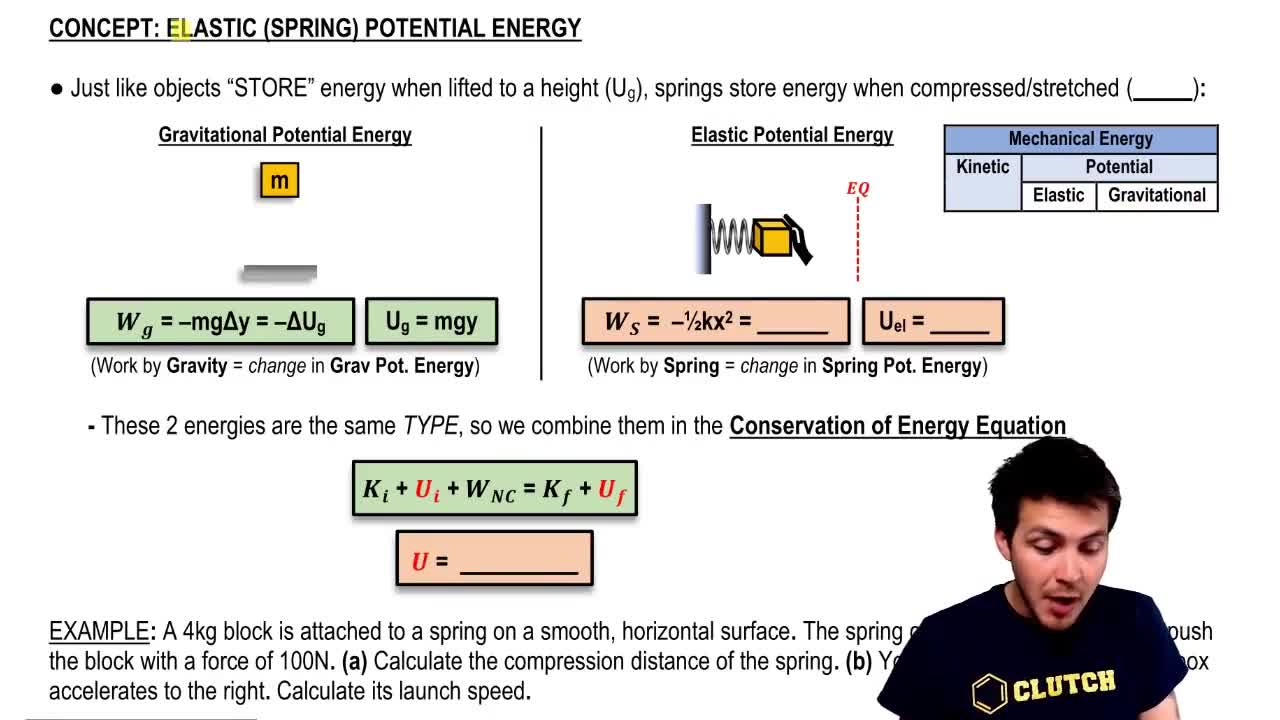
Potential Energy of a Spring
The potential energy stored in a compressed spring is given by the formula PE_spring = (1/2)kx^2, where k is the spring constant and x is the compression distance. In this scenario, the spring constant is 500 N/m and the spring is compressed by 0.3 m, allowing us to calculate the energy available to propel the package.
Recommended video:
Energy in Horizontal Springs
Conservation of Energy
The principle of conservation of energy states that energy cannot be created or destroyed, only transformed from one form to another. In this case, the potential energy stored in the spring is converted into kinetic energy as the package moves up the ramp, allowing us to relate the energies to find the speed of the package.
Recommended video:
Conservation Of Mechanical Energy
Kinetic Energy
Kinetic energy is the energy of an object in motion, expressed by the formula KE = (1/2)mv^2, where m is the mass and v is the velocity. To find the speed of the package when it reaches the truck, we will equate the kinetic energy to the potential energy converted from the spring, taking into account the height gained on the ramp.
Recommended video:
Intro to Rotational Kinetic Energy