Here are the essential concepts you must grasp in order to answer the question correctly.
Kinematics
Kinematics is the branch of physics that deals with the motion of objects without considering the forces that cause the motion. It involves concepts such as velocity, acceleration, and displacement. In this scenario, understanding the initial velocity of the asteroid and the distance it needs to travel to reach Earth is crucial for calculating the time until impact.
Recommended video:
Newton's Second Law of Motion
Newton's Second Law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass, expressed as F = ma. This principle is essential for analyzing the effect of the rocket's thrust on the asteroid's motion. Although the question asks to ignore gravitational forces, the thrust will alter the asteroid's trajectory and speed, which is vital for understanding the overall dynamics.
Recommended video:
Intro to Forces & Newton's Second Law
Time Calculation
Time calculation in physics often involves determining how long it takes for an object to travel a certain distance at a given speed. In this case, the time until the asteroid impacts Earth can be calculated using the formula time = distance / speed. By applying this formula to the initial conditions of the asteroid's motion, one can find the time until impact, assuming no other forces act on it.
Recommended video:
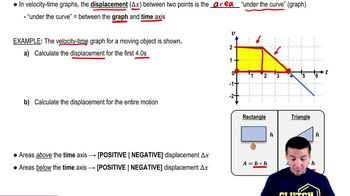
Calculating Displacement from Velocity-Time Graphs