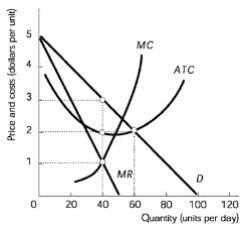
In monopolistic competition, calculating profit involves understanding the relationship between marginal revenue (MR), marginal cost (MC), price, and average total cost (ATC). The key principle is to produce at the quantity where MR equals MC, which is known as the profit-maximizing quantity. This approach is similar to that used in perfect competition, but with the added complexity of a distinct demand curve.
To determine profit or loss, the formula used is:
Profit = (Price - Average Total Cost) × Quantity
This formula calculates profit per unit by subtracting the average total cost from the price, then multiplying by the total number of units sold. If the average total cost is higher than the price, the result will indicate a loss.
To find the profit-maximizing quantity, first identify where the MR curve intersects the MC curve on the graph. This intersection point indicates the optimal quantity to produce. Next, locate the corresponding price on the demand curve and the average total cost on the ATC curve at this quantity. The area between the price and the average total cost, multiplied by the quantity, represents total profit.
In cases of loss, the process is similar. Identify the quantity where MR equals MC, then find the price and average total cost at that quantity. If the average total cost exceeds the price, the area between these two points will represent the loss incurred. The loss-minimizing quantity is the point at which the loss is minimized, ensuring that producing any other quantity would result in a greater loss.
Overall, the analysis of profit and loss in monopolistic competition mirrors that of perfect competition, with the primary distinction being the separate marginal revenue curve. Understanding these concepts is crucial for effectively navigating market structures and making informed business decisions.