Skip to main content
Pearson+ LogoPearson+ Logo
Ch. 4 - Gene Interaction
All textbooksSanders 3rd EditionCh. 4 - Gene InteractionProblem 8
Chapter 4, Problem 8

What is a random sample, and why can a random sample be used to represent a population?

Verified step by step guidance
1
Understand the concept of a random sample: A random sample is a subset of individuals chosen from a larger set (population) where each individual has an equal chance of being selected.
Recognize the importance of randomness: Randomness ensures that the sample is unbiased and representative of the population, minimizing the influence of external factors.
Consider the size of the sample: A sufficiently large random sample can accurately reflect the characteristics of the population, such as mean, variance, and distribution.
Acknowledge the role of random sampling in statistical inference: It allows researchers to make generalizations about the population based on the sample data.
Understand the limitations: While random samples are powerful, they are not foolproof. Sampling errors and biases can still occur, so it's important to use proper sampling techniques and consider the context of the study.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
2m
Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Random Sampling

Random sampling is a technique used in statistics to select a subset of individuals from a larger population, where each individual has an equal chance of being chosen. This method helps to eliminate bias in the selection process, ensuring that the sample accurately reflects the diversity of the entire population.
Recommended video:
Guided course
07:55
Non-Random Mating

Population Representation

A random sample can represent a population because it captures the characteristics of the population without systematic bias. When a sample is randomly selected, it is more likely to include a variety of traits and attributes found in the larger group, allowing researchers to make valid inferences about the population based on the sample data.
Recommended video:
Guided course
05:58
Natural Selection

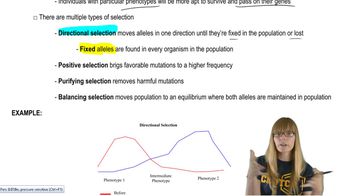
Statistical Inference

Statistical inference is the process of using data from a random sample to make generalizations or predictions about a population. By applying statistical methods, researchers can estimate population parameters, test hypotheses, and draw conclusions, all while accounting for the uncertainty inherent in sampling.
Recommended video:
Guided course
04:55
Overview
Related Practice
Textbook Question

Two genes interact to produce various phenotypic ratios among F₂ progeny of a dihybrid cross. Design a different pathway explaining each of the F₂ ratios below, using hypothetical genes R and T and assuming that the dominant allele at each locus catalyzes a different reaction or performs an action leading to pigment production. The recessive allele at each locus is null (loss-of-function). Begin each pathway with a colorless precursor that produces a white or albino phenotype if it is unmodified. The ratios are for F₂ progeny produced by crossing wild-type F₁ organisms with the genotype RrTt.

15/16 black : 1/16 white

221
views
Textbook Question

Two genes interact to produce various phenotypic ratios among F₂ progeny of a dihybrid cross. Design a different pathway explaining each of the F₂ ratios below, using hypothetical genes R and T and assuming that the dominant allele at each locus catalyzes a different reaction or performs an action leading to pigment production. The recessive allele at each locus is null (loss-of-function). Begin each pathway with a colorless precursor that produces a white or albino phenotype if it is unmodified. The ratios are for F₂ progeny produced by crossing wild-type F₁ organisms with the genotype RrTt.

9/16 black : 3/16 gray : 4/16 albino

218
views
Textbook Question

Two genes interact to produce various phenotypic ratios among F₂ progeny of a dihybrid cross. Design a different pathway explaining each of the F₂ ratios below, using hypothetical genes R and T and assuming that the dominant allele at each locus catalyzes a different reaction or performs an action leading to pigment production. The recessive allele at each locus is null (loss-of-function). Begin each pathway with a colorless precursor that produces a white or albino phenotype if it is unmodified. The ratios are for F₂ progeny produced by crossing wild-type F₁ organisms with the genotype RrTt.

13/16 white : 3/16 green

222
views
Textbook Question

Why is heritability an important phenomenon in plant and animal agriculture?

264
views
Textbook Question
Three pairs of genes with two alleles each (A₁ and A₂, B₁ and B₂, and C₁ and C₂) control the height of a plant. The alleles of these genes have an additive relationship: Each copy of alleles A₁, B₁, and C₁ contributes 6 cm to plant height, and each copy of alleles A₂, B₂, and C₂ contributes 3 cm. What height is expected in the F₁ progeny of a cross between A₁A₁B₁B₁C₁C₁ and A₂A₂B₂B₂C₂C₂.
252
views
Textbook Question

Three pairs of genes with two alleles each (A₁ and A₂, B₁ and B₂, and C₁ and C₂) control the height of a plant. The alleles of these genes have an additive relationship: Each copy of alleles A₁, B₁, and C₁ contributes 6 cm to plant height, and each copy of alleles A₂, B₂, and C₂ contributes 3 cm.

What are the expected heights of plants with each of the homozygous genotypes A₁A₁B₁B₁C₁C₁ and A₂A₂B₂B₂C₂C₂. 

249
views