Ionization involves completely removing an electron from an atom. How much energy is required to ionize a hydrogen atom in its ground (or lowest energy) state? What wavelength of light contains enough energy in a single photon to ionize a hydrogen atom?
Suppose that, in an alternate universe, the possible values of ml are the integer values including 0 ranging from -l -1 to l +1 (instead of simply -l to +l). How many orbitals exist in each sublevel? a. s sublevel b. p sublevel c. d sublevel
 Verified step by step guidance
Verified step by step guidance
Verified Solution
Key Concepts
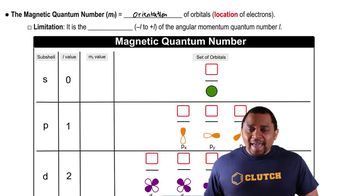
Quantum Numbers

Sublevels and Orbitals

Modified Magnetic Quantum Number
The energy required to ionize sodium is 496 kJ/mol. What minimum frequency of light is required to ionize sodium?
Suppose that in an alternate universe, the possible values of l are the integer values from 0 to n (instead of 0 to n - 1). Assuming no other differences between this imaginary universe and ours, how many orbitals would exist in each level? a. n = 1 b. n = 2 c. n = 3
An atomic emission spectrum of hydrogen shows three wavelengths: 1875 nm, 1282 nm, and 1093 nm. Assign these wavelengths to transitions in the hydrogen atom.
An atomic emission spectrum of hydrogen shows three wavelengths: 121.5 nm, 102.6 nm, and 97.23 nm. Assign these wavelengths to transitions in the hydrogen atom.
The speed of sound in air is 344 m/s at room temperature. The lowest frequency of a large organ pipe is 30 s–1 and the highest frequency of a piccolo is 1.5×104 s–1. Find the difference in wavelength between these two sounds.
