When 10.00 g of phosphorus is burned in O2(g) to form P4O10(s), enough heat is generated to raise the temperature of 2950 g of water from 18.0 °C to 38.0 °C. Calculate the enthalpy of formation of P4O10(s) under these conditions.
Ch.7 - Thermochemistry
Chapter 7, Problem 123
A gaseous fuel mixture contains 25.3% methane (CH4), 38.2% ethane (C2H6), and the rest propane (C3H8) by volume. When the fuel mixture contained in a 1.55 L tank, stored at 755 mmHg and 298 K, undergoes complete combustion, how much heat is emitted? (Assume that the water produced by the combustion is in the gaseous state.)
 Verified step by step guidance
Verified step by step guidance1
Determine the volume of each gas in the mixture by multiplying the total volume of the mixture by the percentage of each component. For example, calculate the volume of methane by multiplying 1.55 L by 25.3%.
Use the ideal gas law, PV = nRT, to calculate the number of moles of each gas. Here, P is the pressure in atmospheres (convert 755 mmHg to atm), V is the volume of each gas, R is the gas constant (0.0821 L atm/mol K), and T is the temperature in Kelvin.
Write the balanced chemical equations for the combustion of methane, ethane, and propane. For methane: CH4 + 2O2
ightarrow CO2 + 2H2O. For ethane: 2C2H6 + 7O2
ightarrow 4CO2 + 6H2O. For propane: C3H8 + 5O2
ightarrow 3CO2 + 4H2O.
Calculate the amount of heat released from the combustion of each gas using the stoichiometry of the reactions and the standard enthalpy changes of combustion for methane, ethane, and propane. Multiply the moles of each gas by the respective \\(\\Delta H_{comb}\\) values.
Sum the heat quantities from each gas to find the total heat emitted from the combustion of the fuel mixture.

Verified Solution
Video duration:
18mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Combustion Reactions
Combustion reactions are exothermic processes where a fuel reacts with an oxidant, typically oxygen, to produce heat, carbon dioxide, and water. In this case, the combustion of methane, ethane, and propane will release energy as they react with oxygen. Understanding the stoichiometry of these reactions is crucial for calculating the heat emitted.
Recommended video:
Guided course
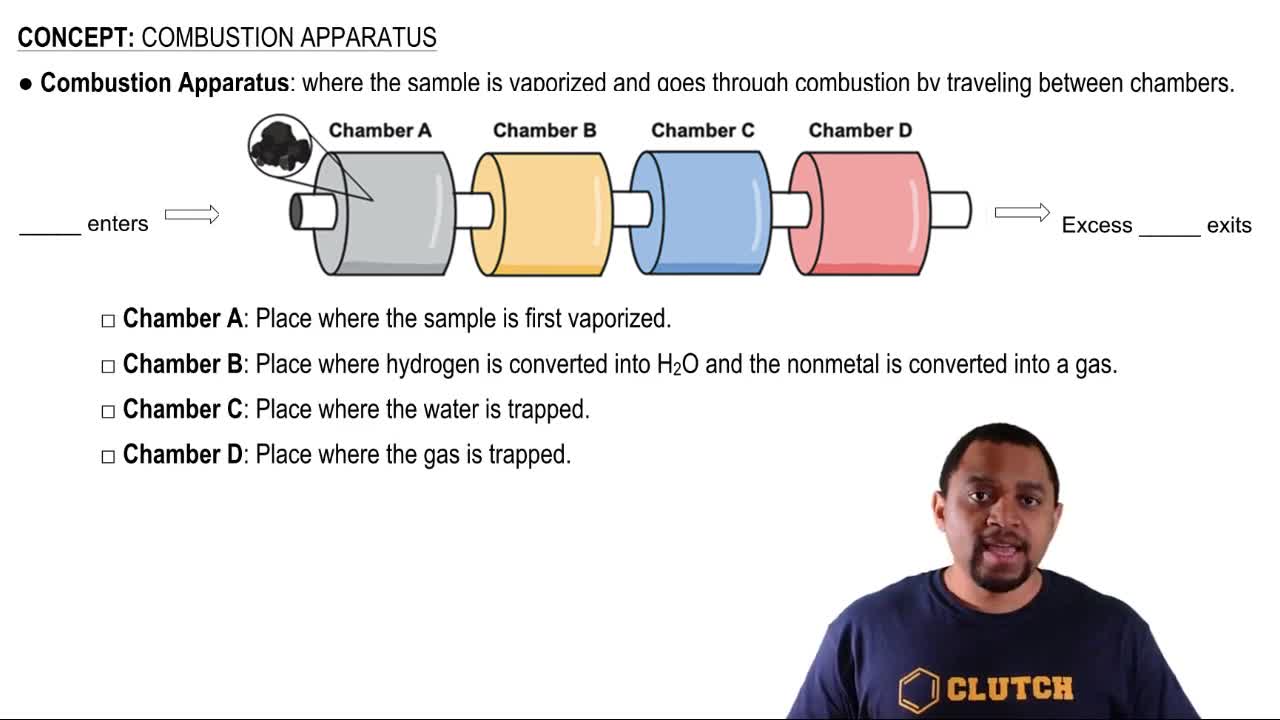
Combustion Apparatus
Ideal Gas Law
The Ideal Gas Law (PV=nRT) relates the pressure, volume, temperature, and number of moles of a gas. In this problem, it is used to determine the number of moles of the gaseous fuel mixture in the tank under the given conditions of pressure and temperature. This is essential for calculating the amount of each component in the mixture and subsequently the total heat released during combustion.
Recommended video:
Guided course

Ideal Gas Law Formula
Heat of Combustion
The heat of combustion is the amount of energy released when a substance undergoes complete combustion. Each hydrocarbon has a specific heat of combustion value, which can be used to calculate the total heat emitted from the combustion of the fuel mixture. Knowing the composition of the mixture allows for the weighted average of the heats of combustion to be calculated, leading to the total heat output.
Recommended video:
Guided course

Combustion Apparatus
Related Practice
Textbook Question
2187
views
1
comments
Textbook Question
The ΔH for the oxidation of sulfur in the gas phase to SO3 is –204 kJ/mol and for the oxidation of SO2 to SO3 is 89.5 kJ/mol. Find the enthalpy of formation of SO2 under these conditions.
1307
views
Textbook Question
The ΔH°f of TiI3(s) is –328 kJ/mol and the ΔH ° for the reaction 2 Ti(s) + 3 I2(g) → 2 TiI3(s) is –839 kJ. Calculate the ΔH of sublimation of I2(s), which is a solid at 25 °C.
1682
views
Textbook Question
A gaseous fuel mixture stored at 745 mmHg and 298 K contains only methane (CH4) and propane (C3H8). When 11.7 L of this fuel mixture is burned, it produces 769 kJ of heat. What is the mole fraction of methane in the mixture? (Assume that the water produced by the combustion is in the gaseous state.)
1781
views
