One of the nuclides in spent nuclear fuel is U-235, an alpha emitter with a half-life of 703 million years. How long will it take for the amount of U-235 to reach 10.0% of its initial amount?
Ch.21 - Radioactivity & Nuclear Chemistry
Chapter 21, Problem 56
A mammoth skeleton has a carbon-14 decay rate of 0.48 disintegration per minute per gram of carbon (0.48 dis/min • g C). When did the mammoth live? (Assume that living organisms have a carbon-14 decay rate of 15.3 dis/min • g C and that carbon- 14 has a half-life of 5715 yr.)
 Verified step by step guidance
Verified step by step guidance1
Identify the given values: the current decay rate of the mammoth skeleton is 0.48 dis/min \( \cdot \) g C, the decay rate of living organisms is 15.3 dis/min \( \cdot \) g C, and the half-life of carbon-14 is 5715 years.
Use the formula for radioactive decay: \( N = N_0 \times e^{-\lambda t} \), where \( N \) is the current decay rate, \( N_0 \) is the initial decay rate, \( \lambda \) is the decay constant, and \( t \) is the time elapsed.
Calculate the decay constant \( \lambda \) using the half-life formula: \( \lambda = \frac{\ln(2)}{\text{half-life}} \).
Rearrange the decay formula to solve for \( t \): \( t = \frac{\ln(N_0/N)}{\lambda} \).
Substitute the known values into the rearranged formula to calculate the time \( t \) when the mammoth lived.

Verified Solution
Video duration:
5mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Carbon-14 Dating
Carbon-14 dating is a radiometric dating method used to determine the age of organic materials by measuring the amount of carbon-14 they contain. Living organisms absorb carbon-14 from the atmosphere, and when they die, the carbon-14 begins to decay at a known rate, characterized by its half-life. This technique is particularly useful for dating materials up to about 50,000 years old.
Recommended video:
Guided course
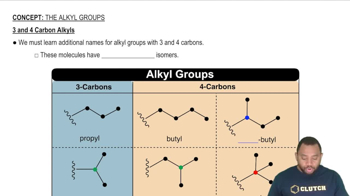
3 and 4 Carbon Alkyls
Half-Life
The half-life of a radioactive isotope is the time required for half of the isotope in a sample to decay into a different element or isotope. For carbon-14, the half-life is approximately 5,715 years. Understanding half-life is crucial for calculating the age of a sample based on the remaining amount of carbon-14 compared to its initial concentration in living organisms.
Recommended video:
Guided course

Zero-Order Half-life
Disintegration Rate
The disintegration rate refers to the number of radioactive decays occurring per unit time, typically expressed in disintegrations per minute (dis/min). In this context, the disintegration rate of carbon-14 in living organisms is higher than in a deceased organism, allowing scientists to estimate the time since death by comparing the current decay rate to the known rate in living organisms.
Recommended video:
Guided course
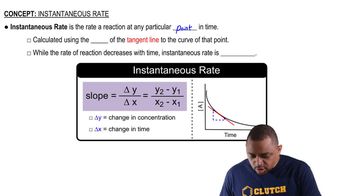
Instantaneous Rate
Related Practice
Textbook Question
2378
views
Textbook Question
A radioactive sample contains 2.35 g of an isotope with a halflife of 3.8 days. What mass of the isotope remains after 7.0 days?
Textbook Question
A sample of F-18 has an initial decay rate of 1.5⨉105/s. How long will it take for the decay rate to fall to 2.5⨉103/s? (F-18 has a half-life of 1.83 hours.)
1680
views
1
rank
Open Question
A rock from Australia contains 0.438 g of Pb-206 for every 1.00 g of U-238. Assuming that the rock did not contain any Pb-206 at the time of its formation, how old is the rock?
Textbook Question
Write the nuclear reaction for the neutron-induced fission of U-235 to form Xe-144 and Sr-90. How many neutrons are produced in the reaction?
690
views
Textbook Question
Write the nuclear reaction for the neutron-induced fission of U-235 to produce Te-137 and Zr-97. How many neutrons are produced in the reaction?
821
views
1
rank
1
comments
