Bromine has two naturally occurring isotopes (Br-79 and Br-81) and has an atomic mass of 79.904 amu. The mass of Br-81 is 80.9163 amu, and its natural abundance is 49.31%. Calculate the mass and natural abundance of Br-79.
Ch.2 - Atoms & Elements
Chapter 2, Problem 88
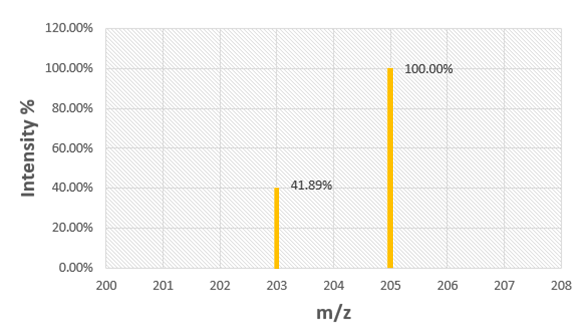
Use the mass spectrum of rubidium to determine the atomic mass of rubidium.

Verified Solution
Video duration:
3mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Mass Spectrum
A mass spectrum is a graphical representation of the mass-to-charge ratio (m/z) of ions. It displays the relative abundance of each ion detected, allowing chemists to identify the composition of a sample. Peaks in the spectrum correspond to different isotopes or molecular fragments, with their heights indicating the intensity or abundance of each ion.
Recommended video:
Guided course

Electromagnetic Spectrum
Atomic Mass
Atomic mass is the weighted average mass of an element's isotopes, measured in atomic mass units (amu). It reflects both the mass and the relative abundance of each isotope present in a sample. To calculate the atomic mass from a mass spectrum, one must consider the m/z values and their corresponding intensity percentages to find a weighted average.
Recommended video:
Guided course

Atomic Mass
Isotopes
Isotopes are variants of a chemical element that have the same number of protons but different numbers of neutrons, resulting in different atomic masses. For rubidium, the isotopes present in the mass spectrum are typically Rb-203, Rb-204, and Rb-205. Understanding isotopes is crucial for accurately determining the atomic mass from the mass spectrum, as each isotope contributes differently based on its abundance.
Recommended video:
Guided course

Isotopes
Related Practice
Textbook Question
8886
views
3
rank
1
comments
Textbook Question
Silicon has three naturally occurring isotopes (Si-28, Si-29, and Si-30). The mass and natural abundance of Si-28 are 27.9769 amu and 92.2%, respectively. The mass and natural abundance of Si-29 are 28.9765 amu and 4.67%, respectively. Find the mass and natural abundance of Si-30.
9413
views
Textbook Question
Use the mass spectrum of europium to determine the atomic mass of europium.
686
views
Textbook Question
How many sulfur atoms are there in 5.52 mol of sulfur?
1811
views
1
rank
Textbook Question
A gold sample contains 4.65×1024 gold atoms. How many moles of gold does the sample contain?
Textbook Question
What is the amount, in moles, of each elemental sample? a. 23.2 g Kr
